Question

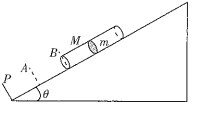
【题目】如图所示，光滑的斜面倾角θ=，斜面底端有一挡板P，斜面固定不动。长为2质量为M的两端开口的圆筒置于斜面上，下端在B点处，PB=2，圆筒的中点处有一质量为m的活塞，M=m。活塞与圆筒壁紧密接触，它们之间的最大静摩擦力与滑动摩擦力相等其值为，其中g为重力加速度的大小。每当圆筒中的活塞运动到斜面上A、B区间时总受到一个沿斜面向上、大小为的恒力作用，AB=。现由静止开始从B点处释放圆筒。

(1)求活塞进入A、B区间前后的加速度大小；

(2)求圆筒第一次与挡板P碰撞前的速度大小和经历的时间；

(3)若圆筒第一次与挡板P碰撞后以原速度大小弹回，活塞离开圆筒后粘在挡板上。那么从圆筒第一次与挡板碰撞到圆筒沿斜面上升到最高点所经历的时间为多少？

Answer 1

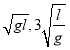【答案】(1)(2)(3)

【解析】

(1)活塞在AB之上时，活塞与筒共同下滑加速度为：

活塞在AB区间内时，假设活塞与筒共同下滑，有：

解得

对m：受向上恒力F=mg，此时有：

解得

故假设成，故活塞的加速度

(2)圆筒下端运动至A处时，活塞刚好到达B点，此时速度为

经历时间t1，由

得

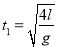
接着M、m一起向下匀速运动，到达P时速度仍为

匀速运动时间为

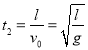
总时间为

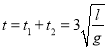
(3)M反弹时刻以υ0上升，m过A点以υ0下滑，以后由于摩擦力和重力，m在M内仍然做匀速下滑，M以加速度

减速，m离开M时间为t3，则有

解得

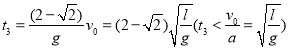
此时M速度为

接着M以加速度

向上减速，有：

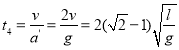
故圆筒沿斜面上升到最高点的时间为