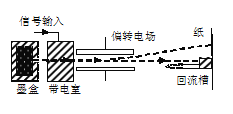
题目内容
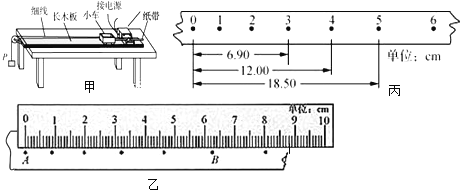
【题目】如图所示,两端有固定挡板的长木板静止在光滑的地面上,总质量M=1g,长度l=0.75m,可视为质点的滑块静止于长木板最右端,滑块质量m=1kg,滑块与长木板间动摩擦因数为μ=04,某时刻长木板以v0=4m/s的速度开始水平向右运动,滑块与挡板间发生的是完全弹性碰撞,g=10m/s2。求:
(1)滑块与挡板发生碰撞的总次数和滑块与木板相对静止时距左侧挡板的距离;
(2)从滑块开始运动到与长木板相对静止的过程中,滑块相对于地面移动的距离。

【答案】(1)0.25m (2)0.75m
【解析】
由动量守恒和功能关系再结合匀变速直线运动规律即可求解。
(1)最终系统以v向右匀速直线运动,根据动量守恒定律有
![]()
由功能关系有
![]()
解得滑块相对于木板移动的距离为s=1m
由于板长l=0.75m,故滑块只与左侧挡板碰撞一次便停在距离左侧挡板0.25m处;
(2)设碰前滑块对地位移为x1,速度为v1,木板对地位移为x2,速度为v2,则有
![]()
![]()
![]()
设碰后滑块与木板速度为![]() ,碰撞过程中有
,碰撞过程中有
![]()
![]()
以后木板匀加速直线运动,滑块匀减速运动,最终速度为v,在此过程中滑块相对地面的位移为![]() ,有
,有
![]()
故从滑块开始运动到与木板相对静止,滑块相对地面的距离为![]() 。
。

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】一同学测量某干电池的电动势和内阻.
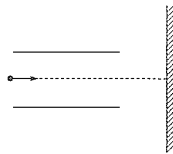
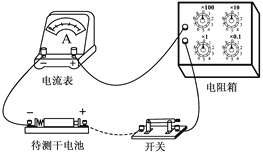
(1)如图所示是该同学正准备接入最后一根导线(图中虚线所示)时的实验电路.请指出图中在器材操作上存在的两个不妥之处__________;____________.
(2)实验测得的电阻箱阻值R和电流表示数I,以及计算的![]() 数据见下表:
数据见下表:
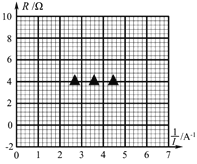
根据表中数据,在答题卡的方格纸上作出![]() 关系图像___________.由图像可计算出该干电池的电动势为_________V;内阻为__________Ω.
关系图像___________.由图像可计算出该干电池的电动势为_________V;内阻为__________Ω.
R/Ω | 8.0 | 7.0 | 6.0 | 5.0 | 4.0 | |
I/A | 0.15 | 0.17 | 0.19 | 0.22 | 0.26 | |
| 6.7 | 6.0 | 5.3 | 4.5 | 3.8 |
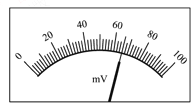
(3)为了得到更准确的测量结果,在测出上述数据后,该同学将一只量程为100 mV的电压表并联在电流表的两端.调节电阻箱,当电流表的示数为0.33 A时,电压表的指针位置如图所示,则该干电池的电动势应为_______V;内阻应为_____Ω.