��Ŀ����
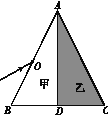
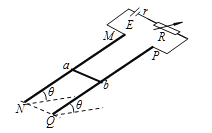
����Ŀ����ͼ��ʾ�����Ϊd��ƽ�е���A2A3��C2C3����ƽ����ˮƽ��ļнǦ�=30�������¶�������ֵΪR�ĵ��裬���ڴŸ�Ӧǿ�ȴ�СΪB������ֱ����ƽ�����ϵ���ǿ�ų��У�ˮƽ̨�����������ų�����Ϊd������Ϊm�ĵ������ֹ�ڹ⻬ˮƽ̨��ACC1A1�ϣ��ڴ�СΪmg(gΪ�������ٶȴ�С)������ˮƽ����ĺ������������ȼ����˶�����ʱ��t��ȥ�����������ǡ���˶������ԵA1C1��Ȼ������ԵA1C1�ɳ�̨�棬��ǡ����A2A3�����䵽A2C2�����ص����»�ʱ��t��ʼ�������˶���������ڵ������˶�ʱʼ���뵼�촹ֱ�ҽӴ����ã����˵���R����������衢һ��Ħ�������ơ���
(1)���������A1C1��ʱ���ٶȴ�Сv0�Լ�A2C2��̨��ACC1A1��ĸ߶Ȳ�h��
(2)����������˶����ٶȴ�Сv��
(3)������ڵ����ϱ��ٻ��еĹ�����ͨ�������ijһ�������ܵ����q��

���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
��������
��1���������̨�������ȼ���ֱ���˶�����ţ�ٵڶ�����������ٶȣ����ٶȹ�ʽ����ٶȣ�������뿪̨�����ƽ���˶���Ӧ��ƽ���˶���������߶ȣ�
��2����E=BLv�����Ӧ�綯�ƣ���ŷķ��������������ɰ�������ʽ����������������������ֱ���˶�����ƽ��������������ٶȣ�
��3��������ڵ������˶����̣�Ӧ�ö��������������ͨ������������ĵ������
��1���������̨�������ȼ���ֱ���˶����ٶȣ�![]() ��
��
��ţ�ٵڶ����ɵã�![]() ��
��
��ã�![]() ��
��
������뿪̨�����ƽ���˶���
��ֱ����![]() ��
��![]() ����ã�
����ã�![]() ��
��
��2��������ڵ�����������ֱ���˶�������ƽ��״̬����ƽ�������ã�![]() ��
��
������![]() ����ã�
����ã�![]() ��
��
��3��������ڵ������˶����̣��ɶ��������ã�![]()
�������![]()
��ã�![]() ��
��