题目内容
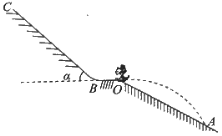
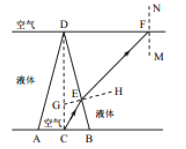
【题目】如图所示，在一个足够宽的槽中盛有折射率为
的液体，中部扣着一个圆锥形透明罩(罩壁极薄)ADB，罩顶角∠ADB=30，高DC=0.2m，罩内为空气，整个罩子没在液体中。槽底AB的中点C处有一点光源，点光源发出的光经折射进入液体后，再从液体上表面射出。不考虑光线在透明罩内部的反射.
求液体表面有光射出的面积(结果保留三位有效数字)。
【答案】S=9.42×10-2m
【解析】如图所示，有一条光线从C点射向DB，在E点折射后进入液体中，射向空气时在F点发生全反射，GH和MN分别为两处的法线GH交CD于G点，∠EFM为临界角C，
则：
，解得：∠C=45
由几何关系得：
，
，
由折射定律可得：
解得：
由几何关系得：
；
在ΔCDE中应用正弦定理：
，
在ADEF中应用正弦定理：
，
解得
，
液体表面有光射出的面积为：
，
解得：
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
