题目内容
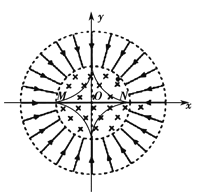
【题目】“太空粒子探测器”是由加速装置、偏转装置和收集装置三部分组成的，其原理可简化如下：如图所示，辐射状的加速电场区域边界为两个同心圆，圆心为O，外圆的半径
，电势
，内圆的半径
，电势
，内圆内有磁感应强度大小
、方向垂直纸面向里的匀强磁场，收集薄板MN与内圆的一条直径重合，收集薄板两端M、N与内圆间各存在狭缝．假设太空中漂浮着质量
、电荷量
的带正电粒子，它们能均匀地吸附到外圆面上，并被加速电场从静止开始加速，进入磁场后，发生偏转，最后打在收集薄板MN上并被吸收(收集薄板两侧均能吸收粒子)，不考虑粒子相互间的碰撞和作用．
(1)求粒子刚到达内圆时速度的大小；
(2)以收集薄板MN所在的直线为
轴建立如图的平面直角坐标系．分析外圆哪些位置 的粒子将在电场和磁场中做周期性运动．指出该位置并求出这些粒子运动一个周期内在磁场中所用时间．
【答案】（1）
(2) 
（0, 2m）,（2m, 0）,（0, -2m）,（-2m, 0）
【解析】（1）带电粒子在电场中被加速时，由动能定理可知
解得： 
（2）粒子进入磁场后，在洛伦兹力的作用下发生偏转，有
解得r=1.0m
因为r=R2，所以由几何关系可知，从收集板左端贴着收集板上表面进入磁场的粒子在磁场中运动
圆周后，射出磁场，进入电场，在电场中先减速后反向加速，并返回磁场，如此反复的周期运动。其运动轨迹如图所示。则在磁场中运动的时间为T。
解得 
粒子进入电场的四个位置坐标分别为（0, 2m）,（2m, 0）,（0, -2m）,（-2m, 0）
练习册系列答案
相关题目
