题目内容
8．
如图所示，装有沙子的A、B两木盒叠放在粗糙的水平桌面上，装沙的小桶C通过细线牵引A、B一起在水平桌面上向右加速运动，设A、B间的摩擦力为f1，B与桌面间的摩擦力为f2．若分别改变A、B、C中沙的质量，则摩擦力f1和f2的变化情况正确的是（ ）| A． | 若只增加C桶中的沙子质量，则f1增加，f2不变 | |
| B． | 若只减少C桶中的沙子质量，则f1减少，f2不变 | |
| C． | 若只增加A箱中的沙子质量，则f1减少，f2不变 | |
| D． | 若只增加B箱中的沙子质量，则f1减少，f2增加 |
分析 物体A与B间是静摩擦力，物体A与桌面间是滑动摩擦力，滑动摩擦力与正压力成正比，静摩擦力随着外力的变化而变化，可以根据牛顿第二定律求解．
解答 解：设物体的加速度大小为a，对A受力分析，受重力、支持力和静摩擦力，根据牛顿第二定律，有：
f1=mAa…①
物体B与桌面间的摩擦力为滑动摩擦力，根据滑动摩擦定律，有
f2=μ（mA+mB）g…②．
A、当沙桶中沙子增加时，加速度增加，静摩擦力f1增加，相对滑动后摩擦力不变，而滑动摩擦力f2不变；故A错误．
B、当沙桶中沙子减小时，加速度减小，静摩擦力f1减小，而滑动摩擦力f2不变；故B正确．
C、若只增加A箱中的沙子质量，f2增大，故C错误．
D、若只增加B箱中的沙子质量，f2增加，加速度减小，则f1减少，故D正确；
故选：BD．
点评 本题关键分清静摩擦力和滑动摩擦力，要明确静摩擦力随着外力的变化而变化，而滑动摩擦力与正压力成正比，不难．
练习册系列答案
相关题目
18．从同一地点先后开出n辆汽车组成车队在平直的公路上行驶，各车均由静止出发先做加速度为a的匀加速直线运动，达到同一速度v后改做匀速直线运动，欲使n辆车都匀速行驶时彼此距离均为s，则各辆车依次启动的时间间隔为（不计汽车的大小）（ ）
| A． | $\frac{2v}{a}$ | B． | $\frac{v}{2a}$ | C． | $\frac{s}{2v}$ | D． | $\frac{s}{v}$ |
19．
如图所示，质量为m的球，被长为L的细绳吊起处于静止状态，现对小球施水平方右的恒力F，小球向右运动到能达到的最高位置时，细绳与竖直立方向的夹角为60°，则恒力F的大小为（ ）
如图所示，质量为m的球，被长为L的细绳吊起处于静止状态，现对小球施水平方右的恒力F，小球向右运动到能达到的最高位置时，细绳与竖直立方向的夹角为60°，则恒力F的大小为（ ）| A． | $\frac{1}{2}$mg | B． | $\frac{\sqrt{3}}{3}$mg | C． | $\frac{\sqrt{3}}{2}$mg | D． | $\sqrt{3}$mg |
16．如图所示，将一根绝缘硬金属导线弯曲成-个完整的正弦曲线形状，它通过两个小金属环a、b与长直金属杆导通，在外力F作用下，正弦形金属线可以在杆上无摩擦滑动．杆的电阻不计，导线电阻为R，a、b间距离为2L，导线组成的正弦图形顶部或底部到杆距离都是$\frac{L}{2}$．在导线和杆平面内有一有界匀强磁场区域，磁场的宽度为L，磁感应强度为B．现在外力F作用下导线沿杆以恒定的速度v向右运动，在运动过程中导线和杆组成的平面始终与磁场垂直．t=0时刻导线从O点进入磁场，直到全部穿过磁场，外力F所做功为（ ）
| A． | $\frac{{B}^{2}{L}^{2}{v}^{2}}{R}$ | B． | $\frac{{B}^{2}{L}^{3}v}{2R}$ | C． | $\frac{3{B}^{2}{L}^{3}v}{4R}$ | D． | $\frac{3{B}^{2}{L}^{2}{v}^{2}}{4R}$ |
3．
如图所示，实线为一列正弦波在某一时刻的波形曲线，经过△t=0.7s，其波形如图中虚线所示，T＜△t＜2T．下列说法正确的是（ ）
如图所示，实线为一列正弦波在某一时刻的波形曲线，经过△t=0.7s，其波形如图中虚线所示，T＜△t＜2T．下列说法正确的是（ ）| A． | 波一定向右传播 | |
| B． | 波速和周期可能为0.5m/s和0.56s | |
| C． | 波速和周期可能为0.7m/s和0.40s | |
| D． | 该波遇到大小为0.2m的障碍物，可以发生明显衍射 | |
| E． | 观察者以某一速度向波源靠近时，接收到的频率可能为1.5 Hz |
13．
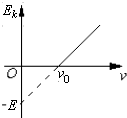如图是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象．由图象可知不正确的是（ ）
如图是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象．由图象可知不正确的是（ ）| A． | 该金属的逸出功等于E | |
| B． | 该金属的逸出功等于hν0 | |
| C． | 入射光的频率为2ν0时，产生的光电子的最大初动能为E | |
| D． | 入射光的频率为$\frac{{v}_{0}}{2}$时，产生的光电子的最大初动能为$\frac{E}{2}$ |
6．人造卫星绕地球的运动可看做匀速圆周运动，已知地球的半径为R，质量为M，自转角速度为ω，万有引力常量为G，地球同步卫星与地球表面间的距离为h，下列计算错误的是（ ）
| A． | 地球近地卫星做匀速圆周运动的线速度为ωR | |
| B． | 地球近地卫星做匀速圆周运动的线速度为$\sqrt{\frac{GM}{R}}$ | |
| C． | 地球同步卫星的运行速度大小为ω（R+h） | |
| D． | 地球同步卫星的运行速度大小为$\sqrt{\frac{GM}{R+h}}$ |
测量两只内阻未知的电流表的内阻，给出下列器材：