题目内容
6.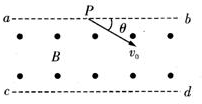 如图所示,匀强磁场垂点于纸面向外,磁场的边界ab、cd平行.现有一带电量为+q的粒子沿纸面从ab边界的某点P射入磁场,粒子速度大小为v0,方向与ab边界成θ=30°角.粒子从cd边界射出时,速度方向与cd边界垂直,已知磁感应强度大小为B,区域足够大,粒子质量为m,不计粒子所受重力.求:
如图所示,匀强磁场垂点于纸面向外,磁场的边界ab、cd平行.现有一带电量为+q的粒子沿纸面从ab边界的某点P射入磁场,粒子速度大小为v0,方向与ab边界成θ=30°角.粒子从cd边界射出时,速度方向与cd边界垂直,已知磁感应强度大小为B,区域足够大,粒子质量为m,不计粒子所受重力.求:(1)粒子从P点刚进入磁场时所受洛伦兹力的大小,并在图中画出方向;
(2)磁场的边界ab、cd的距离及粒子穿越磁场的时间.
分析 (1)根据洛伦兹力公式f=qvB求洛伦兹力大小,由左手定则判断洛伦兹力方向;
(2)根据洛伦兹力提供向心力求出半径和周期表达式,由几何关系找出半径与边界距离关系,联立方程可求出边界距离;由公式$t=\frac{θ}{2π}T$或$t=\frac{θ°}{360°}T$秋李子在磁场中运动的时间.
解答  解:(1)粒子从P点刚进入磁场时洛伦兹力大小为:${f}_{洛}^{\;}=q{v}_{0}^{\;}B$
解:(1)粒子从P点刚进入磁场时洛伦兹力大小为:${f}_{洛}^{\;}=q{v}_{0}^{\;}B$
洛伦兹力方向如图所示
(2)画出粒子在磁场中的运动轨迹,如图所示,根据几何关系,圆弧所对的圆心角为60°,设ab、cd间的距离为d,则有:
$sin60°=\frac{d}{R}$…①
根据洛伦兹力提供向心力,有:
$q{v}_{0}^{\;}B=m\frac{{v}_{0}^{2}}{R}$
得$R=\frac{m{v}_{0}^{\;}}{qB}$…②
联立①②得:$d=\frac{\sqrt{3}m{v}_{0}^{\;}}{2qB}$
粒子运动的周期为:$T=\frac{2πR}{{v}_{0}^{\;}}=\frac{2πm}{qB}$
粒子在磁场中运动的时间为:$t=\frac{60°}{360°}T=\frac{1}{6}×\frac{2πm}{qB}=\frac{πm}{3qB}$
答:(1)粒子从P点刚进入磁场时所受洛伦兹力的大小$q{v}_{0}^{\;}B$,方向如上图;
(2)磁场的边界ab、cd的距离$\frac{\sqrt{3}m{v}_{0}^{\;}}{2qB}$及粒子穿越磁场的时间$\frac{πm}{3qB}$.
点评 本题解题的关键在于画出粒子运动轨迹,分析粒子圆周运动周期与磁场变化周期的关系.粒子圆周运动的时间往往根据轨迹的圆心角与周期的关系确定,t=$\frac{θ}{2π}$T,θ为转过的圆心角

 阅读快车系列答案
阅读快车系列答案| A. | 由于液体表面分子间距离大于液体内部分子间的距离,液面分子间只有引力,没有斥力,所以液体表面具有收缩的趋势 | |
| B. | 液晶既具有液体的流动性,又具有光学各向异性 | |
| C. | 具有规则几何形状的物体一定是晶体 | |
| D. | 有的物质能够生成多种不同的晶体,因为它们的物质微粒能够形成不同的空间结构 |
 如图所示为某个电场的部分电场线,把A、B两点的场强记作EA、EB,A、B两点的电势分别记作φA、φB,则( )
如图所示为某个电场的部分电场线,把A、B两点的场强记作EA、EB,A、B两点的电势分别记作φA、φB,则( )| A. | φA>φB,EA>EB | B. | φA<φB,EA<EB | C. | φA>φB,EA<EB | D. | φA<φB,EA>EB |
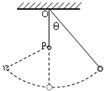 如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点,钉了一颗钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子的瞬间( )
如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点,钉了一颗钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子的瞬间( )| A. | 小球的瞬时速度变大 | B. | 小球的加速度变大 | ||
| C. | 小球的角速度变大 | D. | 悬线所受的拉力变大 |
 (双选)质量为m的物体从高处静止释放后竖直下落,在某时刻受到的空气阻力为f,加速度大小为a=$\frac{g}{3}$,则f的大小是( )
(双选)质量为m的物体从高处静止释放后竖直下落,在某时刻受到的空气阻力为f,加速度大小为a=$\frac{g}{3}$,则f的大小是( )| A. | $\frac{mg}{3}$ | B. | $\frac{2mg}{3}$ | C. | mg | D. | $\frac{4mg}{3}$ |
 2016年CCTV-1综合频道在黄金时间播出了电视剧《陆军一号》,其中直升机抢救伤员的情境深深感动了观众.假设直升机放下绳索吊起伤员后(如图甲所示),竖直方向的速度图象和水平方向的位移图象分别如图乙、丙所示,若不计空气阻力,则( )
2016年CCTV-1综合频道在黄金时间播出了电视剧《陆军一号》,其中直升机抢救伤员的情境深深感动了观众.假设直升机放下绳索吊起伤员后(如图甲所示),竖直方向的速度图象和水平方向的位移图象分别如图乙、丙所示,若不计空气阻力,则( )| A. | 伤员一直处于失重状态 | |
| B. | 绳索中拉力方向一定沿竖直向上 | |
| C. | 地面上观察到伤员的运动轨迹是一条倾斜向上的直线 | |
| D. | 绳索中拉力先大于重力,后小于重力 |
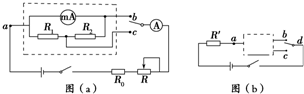
 对改装电表的3mA挡进行校准,校准时需选取的刻度为0.5、1.0、1.5、2.0、2.5、3.0mA.电池的电动势为1.5V,内阻忽略不计;定值电阻R0有两种规格,阻值分别为300Ω和1 000Ω;滑动变阻器R有两种规格,最大阻值分别为750Ω和3000Ω.则R0应选用阻值为300Ω的电阻,R应选用最大阻值为3000Ω的滑动变阻器.
对改装电表的3mA挡进行校准,校准时需选取的刻度为0.5、1.0、1.5、2.0、2.5、3.0mA.电池的电动势为1.5V,内阻忽略不计;定值电阻R0有两种规格,阻值分别为300Ω和1 000Ω;滑动变阻器R有两种规格,最大阻值分别为750Ω和3000Ω.则R0应选用阻值为300Ω的电阻,R应选用最大阻值为3000Ω的滑动变阻器. 如图所示,真空中有Q=8.0×10-5C的点电荷,在距离r=2.0cm的A位置有一电荷量q=+1.0×10-9C的检验电荷.已知静电力常量k=9.0×109N•m2/C2.求:
如图所示,真空中有Q=8.0×10-5C的点电荷,在距离r=2.0cm的A位置有一电荷量q=+1.0×10-9C的检验电荷.已知静电力常量k=9.0×109N•m2/C2.求: 如图所示,A、B、C三点在一条直线上,各点都有一个点电荷,它们所带电量相等.A、B两处为正电荷,C处为负电荷,且BC=2AB,那么A、B、C三个点电荷所受库仑力的大小之比为32:45:13.
如图所示,A、B、C三点在一条直线上,各点都有一个点电荷,它们所带电量相等.A、B两处为正电荷,C处为负电荷,且BC=2AB,那么A、B、C三个点电荷所受库仑力的大小之比为32:45:13.