题目内容
11.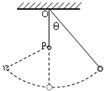 如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点,钉了一颗钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子的瞬间( )
如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点,钉了一颗钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子的瞬间( )| A. | 小球的瞬时速度变大 | B. | 小球的加速度变大 | ||
| C. | 小球的角速度变大 | D. | 悬线所受的拉力变大 |
分析 由机械能守恒可知小球到达最低点的速度,小球碰到钉子后仍做圆周运动,由向心力公式可得出绳子的拉力与小球转动半径的关系;由圆周运动的性质可知其线速度、角速度及向心加速度的大小关系.
解答 解:A、小球摆下后由机械能守恒可知,mgh=$\frac{1}{2}$mv2,因小球下降的高度相同,故小球到达最低点时的速度相同,故小球的线速度不变,故A错误;
B、小球的向心加速度a=$\frac{{v}^{2}}{R}$,R<L,故小球的向心加速度增大,故B正确;
C、根据ω=$\frac{v}{R}$可知,v不变,R变小,故ω变大,故C正确;
D、设钉子到球的距离为R,则F-mg=m$\frac{{v}^{2}}{R}$,故绳子的拉力F=mg+m$\frac{{v}^{2}}{R}$,因R小于L,故有钉子时,绳子上的拉力变大,故D正确;
故选:BCD.
点评 本题考查向心力的计算问题,要注意细绳碰到钉子前后转动半径的变化,明确速度不变,从而明确各物理量的变化,再由向心力公式分析绳子上的拉力变化.

练习册系列答案
相关题目
1.在“验证机械能守恒定律”的实验中,小明同学利用传感器设计实验:如图甲所示,将质量为m、直径为d的金属小球在一定高度h由静止释放,小球正下方固定一台红外线计时器,能自动记录小球挡住红外线的时间t,改变小球下落高度h,进行多次重复实验.此方案验证机械能守恒定律方便快捷.
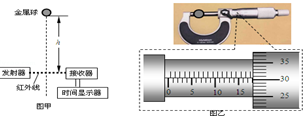
(1)用螺旋测微器测小球的直径如图乙所示,则小球的直径d=17.805;
(2)为直观判断小球下落过程中机械能是否守恒,应作下列哪一个图象D
(3)经正确的实验操作,小明发现小球动能增加量$\frac{1}{2}$mv2总是稍小于重力势能减少量mgh,你认为增加释放高度h后,两者的差值会增大(填“增大”、“缩小”或“不变”).

(1)用螺旋测微器测小球的直径如图乙所示,则小球的直径d=17.805;
(2)为直观判断小球下落过程中机械能是否守恒,应作下列哪一个图象D
| A.h-t图象 | B.h-$\frac{1}{t}$图象 | C.h-t2图象 | D.h-$\frac{1}{{t}^{2}}$图象 |
19.下列固体中全是由晶体组成的是( )
| A. | 石英、云母、明矾、食盐 | B. | 石英、玻璃、云母、铜 | ||
| C. | 食盐、雪花、云母、松香 | D. | 蜂蜡、松香、橡胶、沥青 |
16.下列说法正确的是( )
| A. | 电子的发现表明原子核有复杂结构 | |
| B. | 天然放射性的发现表明原子核有复杂结构 | |
| C. | α粒子散射实验证明了原子的核式结构 | |
| D. | 氢原子光谱表明氢原子的能量是不连续的 |
3.下列说法正确的是( )
| A. | 单晶体和多晶体都有各项异性的物理性质 | |
| B. | 夏天荷叶上小水珠呈球状,说明水不浸润荷叶 | |
| C. | 能量耗散说明能量在不断减小 | |
| D. | 绝对湿度一定的情况下,温度越高相对湿度越大 |
20.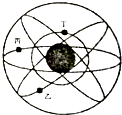 北斗系统的卫星由若干周期为24h的地球静止轨道卫星(如图中丙)、倾斜地球同步轨道卫星(如图中乙)和中圆地球轨道卫员(如图中丁)三种轨道卫星组成,设定它们都绕地心作匀速圆周运动.甲是地球赤道上的一个物体(图中未画出).下列说法中正确的是( )
北斗系统的卫星由若干周期为24h的地球静止轨道卫星(如图中丙)、倾斜地球同步轨道卫星(如图中乙)和中圆地球轨道卫员(如图中丁)三种轨道卫星组成,设定它们都绕地心作匀速圆周运动.甲是地球赤道上的一个物体(图中未画出).下列说法中正确的是( )
 北斗系统的卫星由若干周期为24h的地球静止轨道卫星(如图中丙)、倾斜地球同步轨道卫星(如图中乙)和中圆地球轨道卫员(如图中丁)三种轨道卫星组成,设定它们都绕地心作匀速圆周运动.甲是地球赤道上的一个物体(图中未画出).下列说法中正确的是( )
北斗系统的卫星由若干周期为24h的地球静止轨道卫星(如图中丙)、倾斜地球同步轨道卫星(如图中乙)和中圆地球轨道卫员(如图中丁)三种轨道卫星组成,设定它们都绕地心作匀速圆周运动.甲是地球赤道上的一个物体(图中未画出).下列说法中正确的是( )| A. | 它们运动的向心加速度大小关系是a乙=a丙<a丁<a甲 | |
| B. | 它们运动的线速度大小关系是v甲<v乙=v丙<v丁 | |
| C. | 己知甲运动的周期T甲=24h,可求出地球的密度ρ=$\frac{3π}{G{{T}_{甲}}^{2}}$ | |
| D. | 己知丁运动的周期T丁及轨道半径r丁,可求出地球质量M=$\frac{4{π}^{2}{{r}_{丁}}^{2}}{G{{T}_{丁}}^{2}}$ |
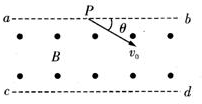 如图所示,匀强磁场垂点于纸面向外,磁场的边界ab、cd平行.现有一带电量为+q的粒子沿纸面从ab边界的某点P射入磁场,粒子速度大小为v0,方向与ab边界成θ=30°角.粒子从cd边界射出时,速度方向与cd边界垂直,已知磁感应强度大小为B,区域足够大,粒子质量为m,不计粒子所受重力.求:
如图所示,匀强磁场垂点于纸面向外,磁场的边界ab、cd平行.现有一带电量为+q的粒子沿纸面从ab边界的某点P射入磁场,粒子速度大小为v0,方向与ab边界成θ=30°角.粒子从cd边界射出时,速度方向与cd边界垂直,已知磁感应强度大小为B,区域足够大,粒子质量为m,不计粒子所受重力.求: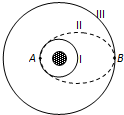 如图所示是发射地球同步卫星的简化轨道示意图,先将卫星发射至距地面高度为h1的近地圆轨道Ⅰ上,在卫星过A点时点火实施变轨,进入远地点为B的椭圆轨道Ⅱ上,过B点时再次点火,将卫星送入地球同步圆轨道Ⅲ.已知地球表面的重力加速度为g,地球自转周期为T,地球半径为R.求:
如图所示是发射地球同步卫星的简化轨道示意图,先将卫星发射至距地面高度为h1的近地圆轨道Ⅰ上,在卫星过A点时点火实施变轨,进入远地点为B的椭圆轨道Ⅱ上,过B点时再次点火,将卫星送入地球同步圆轨道Ⅲ.已知地球表面的重力加速度为g,地球自转周期为T,地球半径为R.求: