题目内容
16.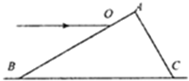 如图所示,ABC为一折射率n=$\sqrt{3}$的直角三棱镜的横截面,∠ABC=30°,∠ACB=60°,长为L的斜边BC放在水平地面上,一细束单色光从AB边距A点$\frac{L}{4}$处的O点平行于BC边射入该棱镜,光线到达地面上的P点(图中未标注).
如图所示,ABC为一折射率n=$\sqrt{3}$的直角三棱镜的横截面,∠ABC=30°,∠ACB=60°,长为L的斜边BC放在水平地面上,一细束单色光从AB边距A点$\frac{L}{4}$处的O点平行于BC边射入该棱镜,光线到达地面上的P点(图中未标注).(1)画出光线从A点到达P点的光路图;
(2)求P点与C的距离.
分析 (1)先根据折射定律$n=\frac{sini}{sinr}$求出光线在AB面上的折射角,由几何知识得到光线射到AC面上的入射角,再根据全反射的条件判断出是否发生全反射,然后画出光路图;
(2)由几何关系结合折射定律求解P点与C的距离.
解答 解:(1)由于∠ABC=30°,一细束单色光从AB边距A点$\frac{L}{4}$处的O点平行于BC边射入该棱镜,所以光在AB界面上的入射角是60°,由折射定律:
$\frac{sini}{sinγ}=n=\sqrt{3}$
所以:sinγ=0.5
γ=30°
由几何关系可知,若折射光线到达AC界面的O′点,则:∠AO′O=30°,$\overline{AO′}=\sqrt{3}\overline{AO}=\frac{\sqrt{3}L}{4}<\frac{1}{2}L$
所以光线不能直接射到BC上.光路图如图.
光线在AC界面上的入射角:i′=90°-∠AO′O=90°-30°=60°
$sin60°=\frac{\sqrt{3}}{2}>\frac{1}{n}=\frac{\sqrt{3}}{3}$所以光线将在AC界面上发生全反射,由几何关系可知,反射光线与BC界面垂直.如图.
(2)由几何关系,则:$\overline{PC}=(\overline{AC}-\overline{AO′})sin30°=(\frac{1}{2}L-\frac{\sqrt{3}L}{4})sin30°$=$\frac{2-\sqrt{3}}{8}L$
答:(1)如图;(2)P点与C的距离是$\frac{2-\sqrt{3}}{8}L$.
点评 解决几何光学问题的关键是,根据题意正确画出光路图,然后根据几何关系以及相关物理知识求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.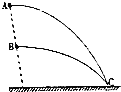 如图所示,A、B两个小球从同一竖直线上的不同位置水平抛出,结果它们落在地面上的同一点C,己知A离地面的高度是B离地面高度的2倍,则A、B两个球的初速度之比vA:vB为( )
如图所示,A、B两个小球从同一竖直线上的不同位置水平抛出,结果它们落在地面上的同一点C,己知A离地面的高度是B离地面高度的2倍,则A、B两个球的初速度之比vA:vB为( )
 如图所示,A、B两个小球从同一竖直线上的不同位置水平抛出,结果它们落在地面上的同一点C,己知A离地面的高度是B离地面高度的2倍,则A、B两个球的初速度之比vA:vB为( )
如图所示,A、B两个小球从同一竖直线上的不同位置水平抛出,结果它们落在地面上的同一点C,己知A离地面的高度是B离地面高度的2倍,则A、B两个球的初速度之比vA:vB为( )| A. | 1:2 | B. | 2:1 | C. | $\sqrt{2}$:1 | D. | $\sqrt{2}$:2 |
11.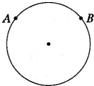 如图所示,若光从A点射入圆形玻璃,经折射从B点射出,已知射出玻璃与射入玻璃的光线夹角为30°,AB弧所对的圆心角为l20°,下列说法中正确的是( )
如图所示,若光从A点射入圆形玻璃,经折射从B点射出,已知射出玻璃与射入玻璃的光线夹角为30°,AB弧所对的圆心角为l20°,下列说法中正确的是( )
 如图所示,若光从A点射入圆形玻璃,经折射从B点射出,已知射出玻璃与射入玻璃的光线夹角为30°,AB弧所对的圆心角为l20°,下列说法中正确的是( )
如图所示,若光从A点射入圆形玻璃,经折射从B点射出,已知射出玻璃与射入玻璃的光线夹角为30°,AB弧所对的圆心角为l20°,下列说法中正确的是( )| A. | 玻璃的折射率为$\sqrt{3}$ | B. | 玻璃的折射率为$\sqrt{2}$ | ||
| C. | 在A点的入射角为30° | D. | 在B点的折射角为45° |
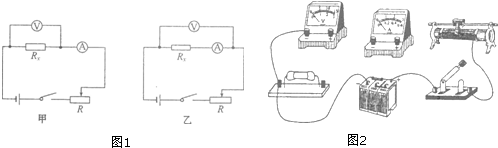
1. 如图所示理想变压器原、副线圈匝数之比为4:1,原线圈接入一电压为U=U0sinωt的交流电源,副线圈接一个R=27.5Ω的负载电阻,若U0=220V,ω=100π rad/s.则下述结论正确的是( )
如图所示理想变压器原、副线圈匝数之比为4:1,原线圈接入一电压为U=U0sinωt的交流电源,副线圈接一个R=27.5Ω的负载电阻,若U0=220V,ω=100π rad/s.则下述结论正确的是( )
 如图所示理想变压器原、副线圈匝数之比为4:1,原线圈接入一电压为U=U0sinωt的交流电源,副线圈接一个R=27.5Ω的负载电阻,若U0=220V,ω=100π rad/s.则下述结论正确的是( )
如图所示理想变压器原、副线圈匝数之比为4:1,原线圈接入一电压为U=U0sinωt的交流电源,副线圈接一个R=27.5Ω的负载电阻,若U0=220V,ω=100π rad/s.则下述结论正确的是( )| A. | 副线圈中电压表的读数为55 V | |
| B. | 副线圈中输出交流电的周期为0.02 s | |
| C. | 原线圈中电流表的读数为0.5 A | |
| D. | 原线圈中的输入功率为55 W |
8.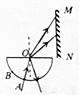 如图,半圆形玻璃砖置于光屏MN的左下方,一束白光沿半径方向从A点射入玻璃砖,在O点发生反射和折射,折射光在白光屏上呈现出彩色光谱.若入射点由A向B缓慢移动,并保持白光沿半径方向入射到O点,观察到各色光在光屏上陆续消失( )
如图,半圆形玻璃砖置于光屏MN的左下方,一束白光沿半径方向从A点射入玻璃砖,在O点发生反射和折射,折射光在白光屏上呈现出彩色光谱.若入射点由A向B缓慢移动,并保持白光沿半径方向入射到O点,观察到各色光在光屏上陆续消失( )
 如图,半圆形玻璃砖置于光屏MN的左下方,一束白光沿半径方向从A点射入玻璃砖,在O点发生反射和折射,折射光在白光屏上呈现出彩色光谱.若入射点由A向B缓慢移动,并保持白光沿半径方向入射到O点,观察到各色光在光屏上陆续消失( )
如图,半圆形玻璃砖置于光屏MN的左下方,一束白光沿半径方向从A点射入玻璃砖,在O点发生反射和折射,折射光在白光屏上呈现出彩色光谱.若入射点由A向B缓慢移动,并保持白光沿半径方向入射到O点,观察到各色光在光屏上陆续消失( )| A. | 在光谱未完全消失之前,反射光的强度逐渐增强 | |
| B. | 最先消失的是红光 | |
| C. | 最先消失的是紫光 | |
| D. | 在玻璃砖中红光的速度最大 |
5.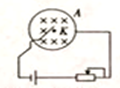 如图所示,在两磁极之间放一培培养皿,磁感线垂直培养皿,皿内侧壁有环状电极A,中心有电极K,皿内装有电解液,若不考虑电解液和培养皿之间的阻力,当通以如图所示电流时,则( )
如图所示,在两磁极之间放一培培养皿,磁感线垂直培养皿,皿内侧壁有环状电极A,中心有电极K,皿内装有电解液,若不考虑电解液和培养皿之间的阻力,当通以如图所示电流时,则( )
 如图所示,在两磁极之间放一培培养皿,磁感线垂直培养皿,皿内侧壁有环状电极A,中心有电极K,皿内装有电解液,若不考虑电解液和培养皿之间的阻力,当通以如图所示电流时,则( )
如图所示,在两磁极之间放一培培养皿,磁感线垂直培养皿,皿内侧壁有环状电极A,中心有电极K,皿内装有电解液,若不考虑电解液和培养皿之间的阻力,当通以如图所示电流时,则( )| A. | 电解液将顺时针旋转流动 | |
| B. | 电解液静止不动 | |
| C. | 若将滑动变阻器的滑片向左移动,则电解液旋转流动将变慢 | |
| D. | 若将磁场的方向和电流的方向均变为和原来相反,则电解液转动方向不变 |
6.一个电量为q=+10-5C的电荷从电场内一点A运动到另一点B,电荷克服电场力做功0.006J(电荷只受电场力作用),在此过程电荷( )
| A. | 电势能增加0.006J | B. | 电势能减少0.006J | ||
| C. | 动能增加0.006J | D. | 动能减少0.006J |
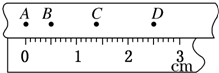 使用电火花计时器分析物体运动情况的实验中:
使用电火花计时器分析物体运动情况的实验中: