题目内容
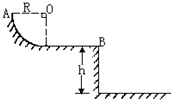 半径R=1m的1/4圆弧轨道下端与一水平轨道连接,水平轨道离地面高度h=1m,如图所示,有一质量m=1.0kg的小滑块自圆轨道最高点A由静止开始滑下,经过水平轨迹末端B时速度为4m/s,滑块最终落在地面上,试求:
半径R=1m的1/4圆弧轨道下端与一水平轨道连接,水平轨道离地面高度h=1m,如图所示,有一质量m=1.0kg的小滑块自圆轨道最高点A由静止开始滑下,经过水平轨迹末端B时速度为4m/s,滑块最终落在地面上,试求:(1)不计空气阻力,滑块落在地面上时速度多大?
(2)滑块在轨道上滑行时克服摩擦力做功多少?
分析:(1)滑块离开B点做平抛运动,根据动能定理求出落地时的速度大小.
(2)对A到B段运用动能定理,求出滑行时克服摩擦力做功的大小.
(2)对A到B段运用动能定理,求出滑行时克服摩擦力做功的大小.
解答:解:(1)根据动能定理得:mgh=
mv2-
mvB2
代入数据解得:v=6m/s.
(2)对A到B运用动能定理得:mgR-Wf=
mvB2-0
解得:Wf=mgR-
mvB2=10×1-
×1×16J=2J.
答:(1)滑块落地时的速度为6m/s.
(2)滑块在轨道上滑行时克服摩擦力做功为2J.
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:v=6m/s.
(2)对A到B运用动能定理得:mgR-Wf=
| 1 |
| 2 |
解得:Wf=mgR-
| 1 |
| 2 |
| 1 |
| 2 |
答:(1)滑块落地时的速度为6m/s.
(2)滑块在轨道上滑行时克服摩擦力做功为2J.
点评:本题考查动能定理的基本运用,动能定理既适用于直线运动,也适用于曲线运动,不需考虑速度的方向,这就是动能定理解题的优越性.

练习册系列答案
相关题目
 如图所示,AB和CD为半径为R=1m的1/4圆弧形光滑轨道,BC为一段长2m的水平轨道.质量为2kg的物体从轨道A端由静止释放,若物体与水平轨道BC间的动摩擦因数为0.1,试求:
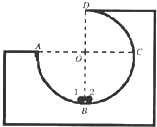
如图所示,AB和CD为半径为R=1m的1/4圆弧形光滑轨道,BC为一段长2m的水平轨道.质量为2kg的物体从轨道A端由静止释放,若物体与水平轨道BC间的动摩擦因数为0.1,试求: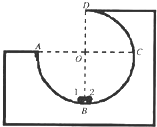 如图所示,在水平面上固定一个半径R=1m的3/4光滑圆弧轨道的工件,其圆心在O点,AOC连线水平,BOD连线竖直.在圆周轨道的最低点B有两个质量分别为m1=4kg,m 2=1kg的可视为质点的小球1和2,两小球间夹有一个极短的轻弹簧,当弹簧储存了EP=90J的弹性势能时锁定弹簧.某时刻解除锁定,弹簧将两个小球弹开,重力加速度g=10m/s2,试求:
如图所示,在水平面上固定一个半径R=1m的3/4光滑圆弧轨道的工件,其圆心在O点,AOC连线水平,BOD连线竖直.在圆周轨道的最低点B有两个质量分别为m1=4kg,m 2=1kg的可视为质点的小球1和2,两小球间夹有一个极短的轻弹簧,当弹簧储存了EP=90J的弹性势能时锁定弹簧.某时刻解除锁定,弹簧将两个小球弹开,重力加速度g=10m/s2,试求: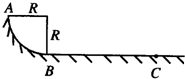 如图所示,半径R=1m的1/4圆弧导轨与水平面相接,从圆弧导轨顶端A,静止释放一个质量为m=20g的小木块,测得其滑至底端B时速度VB=3m/s,以后沿水平导轨滑行BC=3m而停止.
如图所示,半径R=1m的1/4圆弧导轨与水平面相接,从圆弧导轨顶端A,静止释放一个质量为m=20g的小木块,测得其滑至底端B时速度VB=3m/s,以后沿水平导轨滑行BC=3m而停止.