题目内容
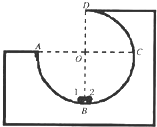 如图所示,在水平面上固定一个半径R=1m的3/4光滑圆弧轨道的工件,其圆心在O点,AOC连线水平,BOD连线竖直.在圆周轨道的最低点B有两个质量分别为m1=4kg,m 2=1kg的可视为质点的小球1和2,两小球间夹有一个极短的轻弹簧,当弹簧储存了EP=90J的弹性势能时锁定弹簧.某时刻解除锁定,弹簧将两个小球弹开,重力加速度g=10m/s2,试求:
如图所示,在水平面上固定一个半径R=1m的3/4光滑圆弧轨道的工件,其圆心在O点,AOC连线水平,BOD连线竖直.在圆周轨道的最低点B有两个质量分别为m1=4kg,m 2=1kg的可视为质点的小球1和2,两小球间夹有一个极短的轻弹簧,当弹簧储存了EP=90J的弹性势能时锁定弹簧.某时刻解除锁定,弹簧将两个小球弹开,重力加速度g=10m/s2,试求:(1)两小球脱离弹簧瞬间的速度
(2)通过计算说明小球2第一次沿轨道上滑过程中能否到达D点?
分析:(1)根据动量守恒定律和机械能守恒定律列式后联立求解即可;
(2)先假设能通过最高点,根据机械能守恒定律求解出最高点速度;然后求解出恰好到最高点的速度;比较两个速度的大小即可.
(2)先假设能通过最高点,根据机械能守恒定律求解出最高点速度;然后求解出恰好到最高点的速度;比较两个速度的大小即可.
解答:解:(1)设小球m1的速度为v1,m2的速度为v2,两个小球与弹簧组成的系统,水平方向合外力为零,且只有弹力做功,由动量守恒定律,有:
m1v1=m2v2 ①
由机械能守恒定律,有;
Ep=
m1v12+
m2v22 ②
联立①②并代入数据解得:v1=3m/s向左
v2=12m/s向右
(2)小球2向右运动,设其能到达原周额最高点D,由机械能守恒,有:
m2
=m2g?2R+
m2
代入数据解得:vD=
m/s
又小球能通过竖直面内光滑圆周最高点的条件为:
mg=m
代入数据解得:v=
m/s
由于v<vD,故小球2能通过最高点.
答:(1)两小球脱离弹簧瞬间的速度分别为:3m/s向左、12m/s向右;
(2)小球2第一次沿轨道上滑过程中能到达D点.
m1v1=m2v2 ①
由机械能守恒定律,有;
Ep=
| 1 |
| 2 |
| 1 |
| 2 |
联立①②并代入数据解得:v1=3m/s向左
v2=12m/s向右
(2)小球2向右运动,设其能到达原周额最高点D,由机械能守恒,有:
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 D |
代入数据解得:vD=
| 104 |
又小球能通过竖直面内光滑圆周最高点的条件为:
mg=m
| v2 |
| R |
代入数据解得:v=
| 10 |
由于v<vD,故小球2能通过最高点.
答:(1)两小球脱离弹簧瞬间的速度分别为:3m/s向左、12m/s向右;
(2)小球2第一次沿轨道上滑过程中能到达D点.
点评:本题关键根据动量守恒定律和机械能守恒定律列式后联立求解,同时明确小球恰好到最高点的临界速度,不难.

练习册系列答案
相关题目
 如图所示,在水平面上向右运动的物体,质量为4kg,物体与水平面的动摩擦因数μ=0.5,在运动过程中,还受到一个水平向左的大小为10N的拉力的作用,则物体受到的滑动摩擦力为(g取10m/s2)( )
如图所示,在水平面上向右运动的物体,质量为4kg,物体与水平面的动摩擦因数μ=0.5,在运动过程中,还受到一个水平向左的大小为10N的拉力的作用,则物体受到的滑动摩擦力为(g取10m/s2)( ) 如图所示,在水平面上有三个质量分别为m1,m2,m3的木块,木块1和2、2和3间分别用一原长为L、劲度系数为K的轻弹簧连接起来,木块1、2与水平面间的动摩擦因数为μ,木块3和水平面之间无摩擦力.现用一水平恒力向右拉木块3,当木块一起匀速运动时,1和3两木块间的距离为(木块大小不计)( )
如图所示,在水平面上有三个质量分别为m1,m2,m3的木块,木块1和2、2和3间分别用一原长为L、劲度系数为K的轻弹簧连接起来,木块1、2与水平面间的动摩擦因数为μ,木块3和水平面之间无摩擦力.现用一水平恒力向右拉木块3,当木块一起匀速运动时,1和3两木块间的距离为(木块大小不计)( ) 如图所示,在水平面上固定三个完全相同的木块,一颗子弹以水平速度v射入,若子弹在木块中做匀减速直线运动,当穿透第三块木块时速度恰好为零,则子弹依次射入每个木块时的速度之比和穿过每个木块所用时间之比分别为( )
如图所示,在水平面上固定三个完全相同的木块,一颗子弹以水平速度v射入,若子弹在木块中做匀减速直线运动,当穿透第三块木块时速度恰好为零,则子弹依次射入每个木块时的速度之比和穿过每个木块所用时间之比分别为( ) (2012?长宁区一模)如图所示,在水平面上放一边长为b的立方体木块M,木块上搁有一根长为l的轻质杆,杆端固定质量为m的均质小球(可视为质点),另一端铰接于O.不计摩擦阻力,由静止释放木块,当杆与水平面间夹角为α时小球获得最大速度,大小为vm.此时杆对木块作用力的大小为
(2012?长宁区一模)如图所示,在水平面上放一边长为b的立方体木块M,木块上搁有一根长为l的轻质杆,杆端固定质量为m的均质小球(可视为质点),另一端铰接于O.不计摩擦阻力,由静止释放木块,当杆与水平面间夹角为α时小球获得最大速度,大小为vm.此时杆对木块作用力的大小为 如图所示,在水平面上有一固定的u形光滑金属框架,框架上放置一金属杆ab.在垂直纸面方向有一匀强磁场,下列情况中可能的是( )
如图所示,在水平面上有一固定的u形光滑金属框架,框架上放置一金属杆ab.在垂直纸面方向有一匀强磁场,下列情况中可能的是( )