Question

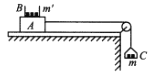
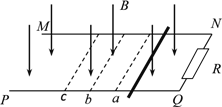
【题目】如图所示，水平放置的光滑平行金属导轨MN、PQ处于竖直向下的足够大的匀强磁场中，导轨间距为L，导轨的右端接有阻值为R的电阻。一根质量为m，电阻为r的金属棒垂直导轨放置，并与导轨接触良好。现使金属棒以一定初速度向左运动，它先后通过位置a、b后，到达位置c处刚好静止。已知磁场的磁感应强度为B，金属棒通过a、b处的速度分别为va、vb，a、b间的距离等于b、c间的距离，导轨的电阻忽略不计。下列说法中正确的是（ ）

A. 金属棒运动到a处时的加速度大小为

B. 金属棒运动到b处时通过电阻的电流方向由N指向Q

C. 金属棒在a→b过程与b→c过程中通过电阻的电荷量相等

D. 金属棒在a处的速度va是其在b处速度vb的倍

Answer 1

【答案】C

【解析】A. 金属棒运动到a处时,有E=BLva,I=E/（R+r）,安培力：F=BIL= ,由牛顿第二定律得加速度：a=F/m=，故A错误；

B. 金属棒运动到b处时，由右手定则判断知，通过电阻的电流方向由Q指向N，故B错误；

C. 金属棒在a→b过程中,通过电阻的电荷量,同理,在b→c的过程中,通过电阻的电荷量,由于△Φab=△Φbc,可得q1=q2.故C正确；

D. 在b→c的过程中,对金属棒运用动量定理得：,而∑v△t=lbc,同理,在a→c的过程中,对金属棒运用动量定理得：,而∑v△t′=lac ,因lac=2lbc,因此va=2vb，故D错误。

故选：C.