题目内容
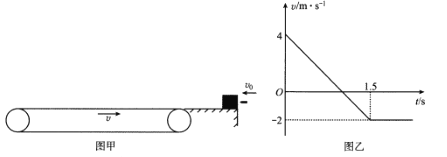
【题目】如图甲所示,有一足够长的水平传送带以v=2 m/s的速度按顺时针方向匀速转动,传送带右端恰好与一段光滑水平面紧挨着,水平地面与传送带上表面处于同一高度,水平面右端有一质量为M=1.9kg的木块处于静止状态。现有一质量m=0.1kg的子弹,以初速度的射入木块,并停留在其中,然后随木块一起向左滑上传送带,木块在传送带上运动的v-t图象如图乙所示(以向左为正方向)。木块可视为质点。取![]() . 求:
. 求:
(1)木块与传送带间的动摩擦因数μ。
(2)子弹射入木块的过程中,子弹与木块组成的系统损失的机械能是多少?
(3)木块在传送带上运动的过程中,电动机多做的功。
【答案】(1)0.4 (2) 304J(3) 24J
【解析】试题分析:(1)由图乙求出0~1.5s的加速度,根据牛顿第二定律求出动摩擦因数;(2)由动量守恒求子弹与木块的共同速度,利用系统的末动能减去系统的初动能求出系统机械能的损失;(3)根据能量守恒可知,电动机多做的功等于传送带克服摩擦カ所做的功。
(1)由图乙可知,在0~1.5s的过程中,木块相对传送带运动,其加速度大小 ![]()
根据牛顿第二定律得:![]()
解得:![]()
(2)子弾进入木块过程中,由动量守恒定律得:![]()
解得:![]()
系统损失的机械能为:![]()
解得:![]()
(3) 0~1.5s的过程中传送带的位移为![]()
则电动机多做的功等于传送带克服摩擦カ所做的功:![]()
解得:![]()

练习册系列答案
相关题目