题目内容
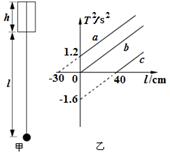
在“用单摆测定重力加速度”的实验中,将一单摆装置竖直悬于某一深度为h(未知)、开口竖直向下的固定小筒中(单摆的下部分露于筒外),如图甲所示。将悬线拉离平衡位置一个小角度后由静止释放,设单摆摆动过程中悬线不会碰到筒壁。如果本实验的长度测量工具只能测量出筒下端口到摆球球心之间的距离l,并通过改变l而测出对应的摆动周期T,再以T2为纵轴、l为横轴,作出T2 - l图象,则可以由此图象得出我们想要测量的物理量。
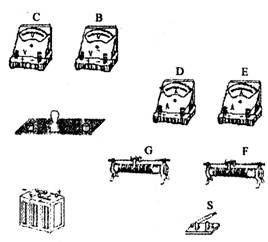
(1)下列工具中,本实验所需的测量工具有_________
A.时钟 B.秒表 C.天平 D.毫米刻度尺
(2)如果实验中所得到的T2 - l关系图象如图乙所示,那么真正的图象应该是a、b、c中的________。
(3)由图象可知,小筒的深度h = _______cm;当地重力加速度g = _____m/s2(π取3.14,计算结果保留三位有效数字)。
【答案】
(1)BD(2)a(2分)(3)30(2分),9.86(2分)
【解析】
试题分析:(1)要测量筒下端口到摆球球心之间的距离以及摆动的周期,所以需要的器材是毫米刻度尺和秒表.故B、D正确,A、C错误.故选BD.
(2)根据 ,图线应该是一条过原点的倾斜直线,但是因为
,图线应该是一条过原点的倾斜直线,但是因为 时,实际摆长不为0,所以图象中
时,实际摆长不为0,所以图象中 时,周期不等于0.故选a
时,周期不等于0.故选a
(3)当 时,对应的位置是-30cm.可知小筒的深度为30cm.图线的斜率
时,对应的位置是-30cm.可知小筒的深度为30cm.图线的斜率 ,所以
,所以 .
.
考点:用单摆测定重力加速度
点评:解决本题的关键掌握单摆的周期公式 ,以及会通过作T2-L图线求重力加速度.
,以及会通过作T2-L图线求重力加速度.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
在《用单摆测定重力加速度》的实验中,某同学测出的g值比当地值大,造成的原因可能是( )
| A、摆角太大了(摆角仍小于10°) | B、量摆长时从悬点量到球的最下端 | C、计算摆长时忘记把小球半径加进去 | D、摆球不是在竖直平面内做简谐振动,而是做圆锥摆运动 | E、计算周期时,将(n-1)次全振动误记为n次全振动 |
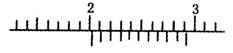
 某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d.
某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d. 某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d.
某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d.