题目内容
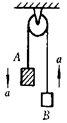
如图所示,轻质弹簧的一端与固定的竖直板P拴接,另一端与物体A相连,物体A置于光滑水平桌面上,A右端连接一细线,细线绕过光滑的定滑轮与物体B相连。开始时托住B,让A处于静止且细线恰好伸直,然后由静止释放B,直至B获得最大速度。下列有关该过程的分析中正确的是( )
| A.B物体受到细线的拉力保持不变 |
| B.B物体机械能的减少量大于弹簧弹性势能的增加量 |
| C.A物体动能的增量等于B物体重力对B做的功与弹簧弹力对A做的功之和 |
| D.A物体与弹簧所组成的系统机械能的增加量等于细线拉力对A做的功 |
BD
解析试题分析: B物体由静止释放,直至B获得最大速度,所以对于A、B和弹簧组成的系统做加速运动,由牛顿第二定律 ,由于x增大,a减小故系统做加速度减小的加速运动,再隔离B有
,由于x增大,a减小故系统做加速度减小的加速运动,再隔离B有 ,绳的拉力T增大,A选项错误;对于A、B和弹簧组成的系统中,由于只有重力和弹簧弹力做功,故系统机械能守恒,B物体机械能的减少量等于弹簧弹性势能的增加量和A物体机械能的增加量,B选项正确;根据动能定理可知,A物体动能的增加量等于弹簧弹力和绳子上拉力对A所做功的代数和,故C错误;由功能关系,系统机械能的增量等于系统除重力和弹簧弹力之外的力所做的功,故A物体与弹簧所组成的系统机械能的增加量等于细线拉力对A做的功,故D选项正确。
,绳的拉力T增大,A选项错误;对于A、B和弹簧组成的系统中,由于只有重力和弹簧弹力做功,故系统机械能守恒,B物体机械能的减少量等于弹簧弹性势能的增加量和A物体机械能的增加量,B选项正确;根据动能定理可知,A物体动能的增加量等于弹簧弹力和绳子上拉力对A所做功的代数和,故C错误;由功能关系,系统机械能的增量等于系统除重力和弹簧弹力之外的力所做的功,故A物体与弹簧所组成的系统机械能的增加量等于细线拉力对A做的功,故D选项正确。
考点:牛顿第二定律 功能关系 动能定理 机械能守恒定律

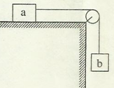
如图所示,带支架的平板小车沿水平面向左做直线运动,小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端,B与小车平板间的动摩擦因数为μ,若细线偏离竖直方向θ角,则小车对物块B产生的作用力的大小和方向为
| A.mg,竖直向上 | B.mg ,斜向左上方 ,斜向左上方 |
| C.mgtanθ,水平向右 | D.mg ,斜向右上方 ,斜向右上方 |
如图所示,绝缘弹簧的下端固定在光滑斜面底端,弹簧与斜面平行,带电小球Q(可视为质点)固定在绝缘斜面上的M点,且在通过弹簧中心的直线ab上。现将与Q大小相同,带电性也相同的小球P,从直线ab上的N点由静止释放,若两小球可视为点电荷,在小球P与弹簧接触到速度变为零的过程中,下列说法中正确的是:
| A.小球P的速度一定先增大后减小 |
| B.小球P的机械能一定在减少 |
| C.小球P速度最大时所受弹簧弹力和库仑力的合力为零 |
| D.小球P与弹簧系统的机械能一定增加 |
如图所示,倾角为 的光滑斜面下端固定一绝缘轻弹簧,M点固定一个质量为m、带电量为-q的小球Q。整个装置处在场强大小为E、方向沿斜面向下的匀强电场中。现把一个带电量为+q的小球P从N点由静止释放,释放后P沿着斜面向下运动。N点与弹簧的上端和M的距离均为s0。P、Q以及弹簧的轴线ab与斜面平行。两小球均可视为质点和点电荷,弹簧的劲度系数为k0,静电力常量为k。则( )
的光滑斜面下端固定一绝缘轻弹簧,M点固定一个质量为m、带电量为-q的小球Q。整个装置处在场强大小为E、方向沿斜面向下的匀强电场中。现把一个带电量为+q的小球P从N点由静止释放,释放后P沿着斜面向下运动。N点与弹簧的上端和M的距离均为s0。P、Q以及弹簧的轴线ab与斜面平行。两小球均可视为质点和点电荷,弹簧的劲度系数为k0,静电力常量为k。则( )
| A.小球P返回时,不可能撞到小球Q |
B.小球P在N点的加速度大小为 |
| C.小球P沿着斜面向下运动过程中,其电势能一定减少 |
D.当弹簧的压缩量为 时,小球P的速度最大 时,小球P的速度最大 |
如图,在密封的盒子内装有一个质量为m的金属球,球刚能在盒内自由活动,若将盒子在空气中竖直向上抛出,则抛出后上升、下降的过程中,以下说法正确的是 
| A.无论空气阻力是否可以忽略,上升都对盒底有压力,下降都对盒顶有压力 |
| B.无论空气阻力是否可以忽略,上升、下降对盒均无压力 |
| C.如果空气阻力不可忽略,则上升、下降均对盒底有压力 |
| D.如果空气阻力不可忽略,升时对盒顶有压力,下降时对盒底有压力; |
如图,小球从高处下落到竖直放置的轻弹簧上,从接触弹簧开始计时到弹簧压缩到最短的过程中,下列叙述正确的是
| A.小球的速度一直减少 |
| B.小球的加速度先减小后增大 |
| C.小球加速度的最大值,小于重力加速度 |
| D.小球机械能守恒 |
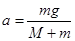
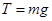
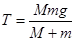

 B.
B.
 D.
D.