题目内容
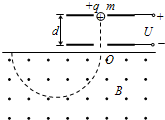
如图所示,两平行金属板间距为d,电势差为U,板间电场可视为匀强电场;金属板下方有一磁感应强度为B的匀强磁场.带电量为+q、质量为m的粒子,由静止开始从正极板出发,经电场加速后射出,并进入磁场做匀速圆周运动.忽略重力的影响,求:
(1)匀强电场场强E的大小;
(2)粒子从电场射出时速度ν的大小;
(3)粒子在磁场中做匀速圆周运动的半径R.
(1)匀强电场场强E的大小;
(2)粒子从电场射出时速度ν的大小;
(3)粒子在磁场中做匀速圆周运动的半径R.

(1)根据匀强电场电势差和电场强度的关系得:
匀强电场场强E的大小E=
;
(2)设带电粒子出电场时速度为v.由动能定理得:Uq=
mv2
解得:v=
; ①
(3)带电粒子在磁场中做匀速圆周运动,由牛顿第二定律得:Bqv=
②
①②联立得:R=
;
答:(1)匀强电场场强E的大小
;(2)粒子从电场射出时速度ν的大小
;(3)粒子在磁场中做匀速圆周运动的半径R
.
匀强电场场强E的大小E=
| U |
| d |
(2)设带电粒子出电场时速度为v.由动能定理得:Uq=
| 1 |
| 2 |
解得:v=
|
(3)带电粒子在磁场中做匀速圆周运动,由牛顿第二定律得:Bqv=
| mv2 |
| R |
①②联立得:R=
| 1 |
| B |
|
答:(1)匀强电场场强E的大小
| U |
| d |
|
| 1 |
| B |
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目