题目内容
如图所示,平行金属板P、Q的中心分别有小孔O和O′,OO′连线与金属板垂直,两板间的电压为U.在Q板的右侧存在匀强磁场,磁场方向垂直纸面向外,磁感应强度为B.磁场右侧边界处的荧光屏MN与Q板间的距离为L,OO′连线的延长线与MN相交于A点.一质量为m、电荷量为+q的带电粒子,从小孔O处由静止开始运动,通过小孔O′后进入磁场,最终打在MN上的A′点.不计粒子重力.求:
(1)带电粒子运动到小孔O′时的速度大小;
(2)A′点与A点之间的距离.

(1)带电粒子运动到小孔O′时的速度大小;
(2)A′点与A点之间的距离.

(1)设粒子运动到小孔O′时的速度大小为υ,根据动能定理得:
qU=
mυ2-0
解得:υ=
(2)粒子通过小孔O′后,在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律:
qυB=m
得:r=
带电粒子在磁场中的运动轨迹以及几何关系如图所示:
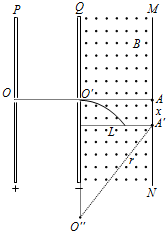
设A′点与A点之间的距离为x,由图可知有:
r2=L2+(r-x)2
解得:x=
-
答:(1)带电粒子运动到小孔O′时的速度大小为
;
(2)A′点与A点之间的距离x=
-
.
qU=
| 1 |
| 2 |
解得:υ=
|
(2)粒子通过小孔O′后,在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律:
qυB=m
| v2 |
| r |
得:r=
| mv |
| qB |
带电粒子在磁场中的运动轨迹以及几何关系如图所示:

设A′点与A点之间的距离为x,由图可知有:
r2=L2+(r-x)2
解得:x=
|
|
答:(1)带电粒子运动到小孔O′时的速度大小为
|
(2)A′点与A点之间的距离x=
|
|

练习册系列答案
相关题目





 跟加速器磁感应强度无关
跟加速器磁感应强度无关