题目内容
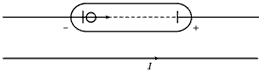
在匀强磁场中置一均匀金属薄片,有一个带电粒子在该磁场中按如图所示轨迹运动.由于粒子穿过金属片时有动能损失,在MN上、下方的轨道半径之比为10:9,不计粒子的重力及空气的阻力,下列判断中正确的是( )

| A.粒子带正电 |
| B.粒子沿abcde方向运动 |
| C.粒子通过上方圆弧比通过下方圆弧时间长 |
| D.粒子恰能穿过金属片10次 |

A、粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:qvB=m
,则粒子的轨道半径:r=
,
由r=
可知,r与带电粒子的运动速度成正比.显然半径大的圆周是穿过金属片前的带电粒子的运动轨迹,半径小的圆周是穿过金属片后的带电粒子的运动轨迹,所以粒子沿edcba方向运动,由左手定则可知,带电粒子带正电,故A正确,B错误;
C、粒子做圆周运动的周期T=
,由周期公式可知,带电粒子在磁场中的运动周期与运动速度无关,故C错误;
D、半径之比为10:9,由r=
可知,粒子的速度之比为10:9,由动能定理可得,粒子能穿过金属片的次数为:n=
,故D错误;
故选:A.
| v2 |
| r |
| mv |
| Bq |
由r=
| mv |
| Bq |
C、粒子做圆周运动的周期T=
| 2πm |
| qB |
D、半径之比为10:9,由r=
| mv |
| Bq |
| 100 |
| 19 |
故选:A.

练习册系列答案
相关题目