题目内容
9.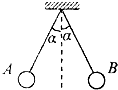 如图,用两根绝缘丝线悬在同一点的带等量电荷的小球(可视为点电荷)受静电斥力而相互分开,两悬线和竖直方向的夹角都为α,两球的质量都为m,两线长都为L,每个小球所带电量都为+q,则q的大小是多少?
如图,用两根绝缘丝线悬在同一点的带等量电荷的小球(可视为点电荷)受静电斥力而相互分开,两悬线和竖直方向的夹角都为α,两球的质量都为m,两线长都为L,每个小球所带电量都为+q,则q的大小是多少?
分析 对其中一个小球受力分析,由共点力的平衡条件可得小球受到的库仑力,由库仑力公式可得出小球所带电荷量.
解答 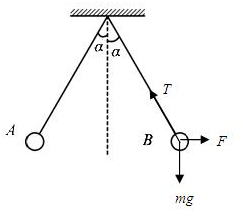 解:对小球进行受力分析,如图所示.设小球在水平方向受到库仑力的大小为F,根据平衡条件得:
解:对小球进行受力分析,如图所示.设小球在水平方向受到库仑力的大小为F,根据平衡条件得:
$\frac{F}{mg}$=tanα
所以:F=mgtanα
根据库仑定律得:F=k$\frac{{q}^{2}}{{r}^{2}}$
有几何关系可知:r=2Lsinα
解得:q=2Lsinα$\sqrt{\frac{mgtanα}{k}}$
答:球所带的电荷量大小是2Lsinα$\sqrt{\frac{mgtanα}{k}}$.
点评 本题两边的球是对称的,故分析其中一个小球即可得出正确结论;在电场中处理问题的方法与力学是一致的,做好受力分析是解决问题的关键.

练习册系列答案
相关题目
19.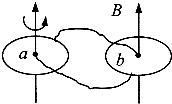 在竖直向上的匀强磁场中,分别放入两个完全相同的带中心轴的水平金属圆盘a和b(圆盘的电阻不能忽略),它们可以绕中心轴自由转动,彼此用导线把中心转轴和对方圆盘的边缘相连接,组成电路如图所示.当圆盘a在外力作用下按如图方向转动时,则( )
在竖直向上的匀强磁场中,分别放入两个完全相同的带中心轴的水平金属圆盘a和b(圆盘的电阻不能忽略),它们可以绕中心轴自由转动,彼此用导线把中心转轴和对方圆盘的边缘相连接,组成电路如图所示.当圆盘a在外力作用下按如图方向转动时,则( )
 在竖直向上的匀强磁场中,分别放入两个完全相同的带中心轴的水平金属圆盘a和b(圆盘的电阻不能忽略),它们可以绕中心轴自由转动,彼此用导线把中心转轴和对方圆盘的边缘相连接,组成电路如图所示.当圆盘a在外力作用下按如图方向转动时,则( )
在竖直向上的匀强磁场中,分别放入两个完全相同的带中心轴的水平金属圆盘a和b(圆盘的电阻不能忽略),它们可以绕中心轴自由转动,彼此用导线把中心转轴和对方圆盘的边缘相连接,组成电路如图所示.当圆盘a在外力作用下按如图方向转动时,则( )| A. | 圆盘b沿与a盘相反的方向转动 | B. | 圆盘b沿与a盘相同的方向转动 | ||
| C. | 圆盘b是一个等势体 | D. | 圆盘b中心电势比边缘电势高 |
20.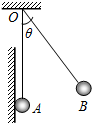 如图所示,小球A、B带电量相等、质量相等(可视为点电荷),都用同样长度的绝缘细线挂在绝缘的竖直墙上O点,A球靠墙且其悬线刚好竖直,B球悬线偏离竖直方向一定角度而静止.由于某种外部原因,两球再次静止时它们之间的距离变为原来的两倍,则下面所列原因中可能正确的是( )
如图所示,小球A、B带电量相等、质量相等(可视为点电荷),都用同样长度的绝缘细线挂在绝缘的竖直墙上O点,A球靠墙且其悬线刚好竖直,B球悬线偏离竖直方向一定角度而静止.由于某种外部原因,两球再次静止时它们之间的距离变为原来的两倍,则下面所列原因中可能正确的是( )
 如图所示,小球A、B带电量相等、质量相等(可视为点电荷),都用同样长度的绝缘细线挂在绝缘的竖直墙上O点,A球靠墙且其悬线刚好竖直,B球悬线偏离竖直方向一定角度而静止.由于某种外部原因,两球再次静止时它们之间的距离变为原来的两倍,则下面所列原因中可能正确的是( )
如图所示,小球A、B带电量相等、质量相等(可视为点电荷),都用同样长度的绝缘细线挂在绝缘的竖直墙上O点,A球靠墙且其悬线刚好竖直,B球悬线偏离竖直方向一定角度而静止.由于某种外部原因,两球再次静止时它们之间的距离变为原来的两倍,则下面所列原因中可能正确的是( )| A. | B的带电量不变,A的带电量变为原来的2倍 | |
| B. | A的带电量不变,B的带电量变为原来的4倍 | |
| C. | B的带电量不变,A的带电量变为原来的8倍 | |
| D. | A的带电量不变,B的带电量变为原来的16倍 |
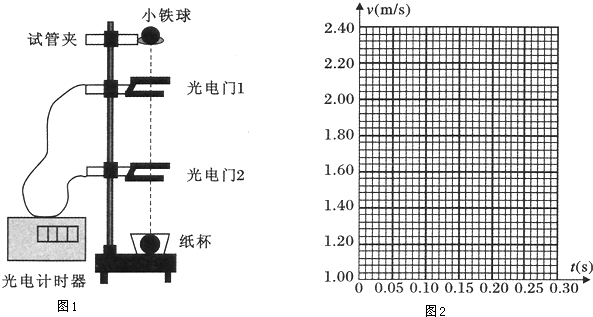
17.某研究性学习小组用图1所示装置来测定当地重力加速度,主要操作如下:
①安装实验器材,调节试管夹(小铁球)、光电门和纸杯在同一竖直线上;
②打开试管夹,由静止释放小铁球,用光电计时器记录小铁球在两个光电门间的运动时间t,并用刻度尺(图上未画出)测量出两个光电门之间的高度h,计算出小铁球通过两光电门间的平均速度v;
③保持光电门1的位置不变,改变光电门2的位置,重复②的操作,测出多组(h,t),计算出对应的平均速度”;
④画出v-t图象.
请根据实验,回答如下问题:
(1)设小铁球到达光电门l时的速度为v0,当地的重力加速度为g.则小铁球通过两光电门间平均速度v的表达式为v=v0+$\frac{1}{2}$gt.(用v0、g和t表示)
(2)实验测得的数据如表:
请在图2坐标纸上画出v-t图象.
(3)根据v-t图象,可以求得当地重力加速度g=9.7m/s2,小球通过光电门1时的速度为1.1m/s.(以上结果均保留两位有效数字)
①安装实验器材,调节试管夹(小铁球)、光电门和纸杯在同一竖直线上;
②打开试管夹,由静止释放小铁球,用光电计时器记录小铁球在两个光电门间的运动时间t,并用刻度尺(图上未画出)测量出两个光电门之间的高度h,计算出小铁球通过两光电门间的平均速度v;
③保持光电门1的位置不变,改变光电门2的位置,重复②的操作,测出多组(h,t),计算出对应的平均速度”;
④画出v-t图象.

请根据实验,回答如下问题:
(1)设小铁球到达光电门l时的速度为v0,当地的重力加速度为g.则小铁球通过两光电门间平均速度v的表达式为v=v0+$\frac{1}{2}$gt.(用v0、g和t表示)
(2)实验测得的数据如表:
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| h(cm) | 10.00 | 20.00 | 30.00 | 40.00 | 50.00 | 60.00 |
| t(s) | 0.069 | 0.119 | 0.159 | 0.195 | 0.226 | 0.255 |
| v(m/s) | 1.45 | 1.68 | 1.89 | 2.05 | 2.21 | 2.35 |
(3)根据v-t图象,可以求得当地重力加速度g=9.7m/s2,小球通过光电门1时的速度为1.1m/s.(以上结果均保留两位有效数字)
19.利用金属导体的电阻随温度变化的特点可以制成电阻温度计.如图甲所示为某种金属导体的电阻R随温度t变化的图线.如果用这种金属导体做成测温探头,再将它连入如图乙所示的电路中,随着测温探头处待测温度的变化,电流表示数也会发生变化.则在t1-t2温度范围内( )
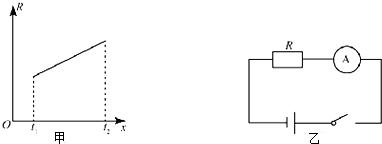

| A. | 待测温度越高,电流表的示数越大 | |
| B. | 待测温度越高,电流表的示数越小 | |
| C. | 待测温度升高,电流表的示数均匀增大 | |
| D. | 待测温度升高,电流表的示数均匀减小 |
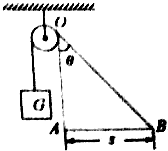 如图所示,一辆拖车通过定滑轮将一重物G匀速提升,当拖车从A点水平移动到B点时,位移s,绳子由竖直变为与竖直方向成θ的角度,求此过程中拖车对绳子所做的功.
如图所示,一辆拖车通过定滑轮将一重物G匀速提升,当拖车从A点水平移动到B点时,位移s,绳子由竖直变为与竖直方向成θ的角度,求此过程中拖车对绳子所做的功. 如图所示,光滑水平桌面上O处有一光滑的圆孔,一根轻绳一端系一质量为M的木块,当小球m以某一角速度在桌面上做匀速圆周运动时,木块M恰能静止不动,这时小球做圆周运动的半径为r,则此时小球做匀速圆周运动的角速度为多大?
如图所示,光滑水平桌面上O处有一光滑的圆孔,一根轻绳一端系一质量为M的木块,当小球m以某一角速度在桌面上做匀速圆周运动时,木块M恰能静止不动,这时小球做圆周运动的半径为r,则此时小球做匀速圆周运动的角速度为多大?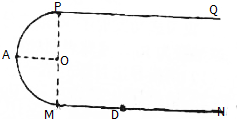 如图所示,一绝缘?形弯杆由两段直杆PQ、MN和一半径为R的半圆环连接组成,固定在纸面所在的竖直平面内,PQ、MN水平且足够长,半圆环MAP段是光滑的,现有一质量为m的小环套在MN杆上.且小环在运动过程中始终受到一个大小为$\frac{3}{4}$mg的水平向左的恒力作用.小环与PQ、MN间动摩擦因数均为0.25,现使小环在距离M点右侧2R的D点以某一初速度向左运动,小环刚好能到达P点,求:
如图所示,一绝缘?形弯杆由两段直杆PQ、MN和一半径为R的半圆环连接组成,固定在纸面所在的竖直平面内,PQ、MN水平且足够长,半圆环MAP段是光滑的,现有一质量为m的小环套在MN杆上.且小环在运动过程中始终受到一个大小为$\frac{3}{4}$mg的水平向左的恒力作用.小环与PQ、MN间动摩擦因数均为0.25,现使小环在距离M点右侧2R的D点以某一初速度向左运动,小环刚好能到达P点,求: