题目内容
1. 如图所示,光滑水平桌面上O处有一光滑的圆孔,一根轻绳一端系一质量为M的木块,当小球m以某一角速度在桌面上做匀速圆周运动时,木块M恰能静止不动,这时小球做圆周运动的半径为r,则此时小球做匀速圆周运动的角速度为多大?
如图所示,光滑水平桌面上O处有一光滑的圆孔,一根轻绳一端系一质量为M的木块,当小球m以某一角速度在桌面上做匀速圆周运动时,木块M恰能静止不动,这时小球做圆周运动的半径为r,则此时小球做匀速圆周运动的角速度为多大?
分析 对M,受力平衡,绳子的拉力等于重力,对m受力分析,绳子的拉力提供A所需的向心力,根据向心力公式T=mω2r即可求解
解答 解:m受重力、支持力、轻绳拉力的共同作用,而重力与支持力平衡,所以轻绳拉力F充当向心力,即F=mrω2.
木块M静止,所以轻绳拉力F=Mg,即Mg=mrω2,所以ω=$\sqrt{\frac{Mg}{mr}}$
答:此时小球做匀速圆周运动的角速度为$\sqrt{\frac{Mg}{mr}}$.
点评 解决本题的关键知道绳子的拉力提供m做圆周运动的向心力,结合M受力分析列出受力平衡方程进行求解,注意研究对象的灵活选择.

练习册系列答案
相关题目
12.下列表述符合物理学史实的是( )
| A. | 开普勒认为只有在一定的条件下,弹簧的弹力才与弹簧的形变量成正比 | |
| B. | 牛顿认为在足够高的山上以足够大的水平速度抛出物体,物体就不会再落到地球上 | |
| C. | 奥斯特发了电磁感应现象,并坚信电和磁之间存在一定的联系 | |
| D. | 安培首先引入电场线和磁感线,极大地促进了他对电磁现象的研究 |
16.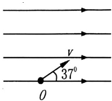 如图所示,一质量为m,电量为q的带电油滴,从水平向右的匀强电场中的O点以速度v沿与场强方向成37°角射入电场中,油滴运动到最高点时速度大小也是v,己知重力加速度为g,下列说法正确的是( )
如图所示,一质量为m,电量为q的带电油滴,从水平向右的匀强电场中的O点以速度v沿与场强方向成37°角射入电场中,油滴运动到最高点时速度大小也是v,己知重力加速度为g,下列说法正确的是( )
 如图所示,一质量为m,电量为q的带电油滴,从水平向右的匀强电场中的O点以速度v沿与场强方向成37°角射入电场中,油滴运动到最高点时速度大小也是v,己知重力加速度为g,下列说法正确的是( )
如图所示,一质量为m,电量为q的带电油滴,从水平向右的匀强电场中的O点以速度v沿与场强方向成37°角射入电场中,油滴运动到最高点时速度大小也是v,己知重力加速度为g,下列说法正确的是( )| A. | 最高点一定在0点的正上方 | |
| B. | 最高点可能在0点的右上方 | |
| C. | 0点与最高点之间的电势差可能为零 | |
| D. | 匀强电场的电场强度E=$\frac{3mg}{q}$ |
10.如图(甲)所示,一根质量分布均匀的粗绳AB长为l,在水平恒力F的作用下沿水平面运动.绳上距A端x处的张力T与x的关系如图(乙)所示(F和l为已知量).下列说法正确的是( )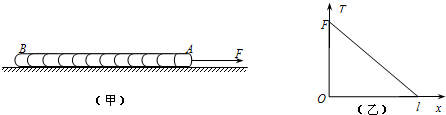

| A. | 粗绳一定不受到摩擦力作用 | |
| B. | 若只增大恒力F,则T-x直线斜率的绝对值变大 | |
| C. | 若已知粗绳的质量,则可求出粗绳运动的加速度 | |
| D. | 若已知粗绳运动的加速度,则可求出粗绳的质量 |
11.下列关于α粒子的说法正确的是( )
| A. | 物理学家卢瑟福通过α粒子散射实验说明了原子核内部有复杂的结构 | |
| B. | 原子核放出α粒子即α衰变,α衰变的核反应方程式为${\;}_{Z}^{A}$X→${\;}_{Z-2}^{A-4}$Y+${\;}_{2}^{4}$He | |
| C. | 原子核放出α粒子即α衰变,α衰变的实质是一个中子转化一个质子和电子 | |
| D. | 比较α、β、γ三种射线,由α粒子组成的α射线,电离能力最弱、穿透能力最强 |
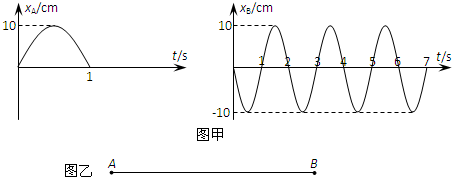
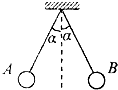 如图,用两根绝缘丝线悬在同一点的带等量电荷的小球(可视为点电荷)受静电斥力而相互分开,两悬线和竖直方向的夹角都为α,两球的质量都为m,两线长都为L,每个小球所带电量都为+q,则q的大小是多少?
如图,用两根绝缘丝线悬在同一点的带等量电荷的小球(可视为点电荷)受静电斥力而相互分开,两悬线和竖直方向的夹角都为α,两球的质量都为m,两线长都为L,每个小球所带电量都为+q,则q的大小是多少?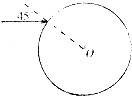 一透明圆柱体截面如图所示,圆心为O,半径为R,一束单色光射入透明圆柱体内,入射角为45°,光线在透明圆柱体内经一次反射后,再次折射回到空气中时相对入射光线偏转150°,已知光在真空中的传播速度为c,求:
一透明圆柱体截面如图所示,圆心为O,半径为R,一束单色光射入透明圆柱体内,入射角为45°,光线在透明圆柱体内经一次反射后,再次折射回到空气中时相对入射光线偏转150°,已知光在真空中的传播速度为c,求: