题目内容
(13分)如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,天文学家观测得到A行星的运行轨道半径为R0,周期为T0.A行星的半径为r0,其表面的重力加速度为g,不考虑行星的自转.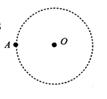
⑴中央恒星O的质量是多大?
⑵若A行星有一颗距离其表面为h做圆周运动的卫星,求该卫星的线速度大小。(忽略恒星对卫星的影响)
⑴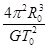 ;⑵
;⑵
解析试题分析:⑴设中央恒星O的质量为M,A行星的质量为m,根据万有引力定律和牛顿第二定律有: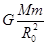 =
=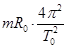
解得中央恒星O的质量为:M=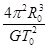
⑵设卫星的质量为m0,卫星的线速度为v,根据万有引力定律和牛顿第二定律有: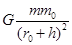 =
=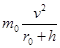
当该卫星位于行星A的表面时,有: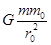 =m0g
=m0g
联立以上两式解得该卫星的线速度大小为:v=
考点:本题主要考查了万有引力定律和牛顿第二定律的应用问题,属于中档题。

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 的光滑斜面上,一劲度系数为k的轻弹簧连接质量分别为m1、m2的甲、乙两小物块.开始时,两物块在光滑挡板作用下静止在斜面上.现作用在乙物块一平行于斜面向上的力,使乙物块以加速度a匀加速运动.问
的光滑斜面上,一劲度系数为k的轻弹簧连接质量分别为m1、m2的甲、乙两小物块.开始时,两物块在光滑挡板作用下静止在斜面上.现作用在乙物块一平行于斜面向上的力,使乙物块以加速度a匀加速运动.问

 的光滑半圆轨道竖直固定在高
的光滑半圆轨道竖直固定在高 的光滑水平台上,与平台平滑连接,平台长
的光滑水平台上,与平台平滑连接,平台长 .可视为质点的两物块
.可视为质点的两物块 、
、 束缚在一起,并静止在平台的最右端D点,它们之间有被压缩的轻质弹簧,某时刻突然解除束缚,使两物块
束缚在一起,并静止在平台的最右端D点,它们之间有被压缩的轻质弹簧,某时刻突然解除束缚,使两物块 ,水平抛出后在水平地面上的落在水平地面上的P点,
,水平抛出后在水平地面上的落在水平地面上的P点, ,
, 取
取 .求:
.求:


 的斜坡,BC是半径为
的斜坡,BC是半径为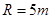 的圆弧面,圆弧面和斜面相切于B,与水平面相切于C,如图所示,AB竖直高度差为
的圆弧面,圆弧面和斜面相切于B,与水平面相切于C,如图所示,AB竖直高度差为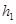 ,竖直台阶CD高度差为
,竖直台阶CD高度差为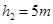 ,台阶底端与倾角为
,台阶底端与倾角为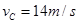 ,通过C点后飞落到DE上(不计空气阻力和轨道的摩擦阻力,
,通过C点后飞落到DE上(不计空气阻力和轨道的摩擦阻力, 取10m/s2,sin37°=0.6,cos37°=0.8).求:
取10m/s2,sin37°=0.6,cos37°=0.8).求: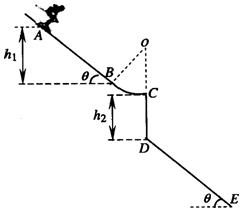
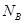 ?
?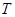 ?
?