题目内容
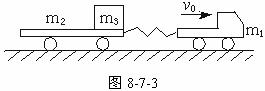
在光滑水平面上,有一质量为m1=20 kg的小车,通过一根几乎不能伸长的轻绳与另一个质量为m2=25 kg的拖车相连接,一质量为m3=15 kg的物体放在拖车的平板上,物体与平板间的动摩擦因数μ=0.2.开始时,拖车处于静止状态,绳未拉紧(如图8- 7- 3所示),小车以v0=3 m/s的速度向前运动.求:(1)当m1、m2、m3以同一速度前进时,其速度的大小;
(2)物体在拖车平板上移动的距离(g取10 m/s2).
解析:(1)研究m1、m2、m3组成的系统.绳子的拉力、m3与m2之间的摩擦力均为内力,外力之和为零,系统的动量守恒.则有
m1v0=(m1+m2+m3)v2
由此解得三者的共同速度v2=![]() =1 m/s.
=1 m/s.
(2)绳绷紧的极短时间内相当于m1和m2碰撞,m3未动,m1、m2动量守恒
m1v0=(m1+m2)v1
由此式解得绳刚拉紧时m1和m2的共同速度v1=![]() =
=![]() m/s
m/s
绳绷紧后,小车和拖车的速度由v1减至v2.设此过程小车和拖车的位移为s1,对小车和拖车由动能定理,有
μm3gs1=![]() (m1+m2)(v12-v22) ①
(m1+m2)(v12-v22) ①
物块的速度由0增至v2,设此过程物块的位移为s2,对物块由动能定理,有
μm3gs2=![]() m3v22 ②
m3v22 ②
设物块在拖车上移动的距离为Δs,则Δs=s1-s2 ③
代入数据由以上三式可解得Δs=0.33 m.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
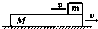 如图所示,在光滑水平面上,有一质量为M=3kg的薄板和质量为m=1kg的物块,都以v=4m/s的初速度朝相反方向运动,它们之间有摩擦,薄板足够长,当薄板的速度为2.4m/s时,物块的运动情况是( )
如图所示,在光滑水平面上,有一质量为M=3kg的薄板和质量为m=1kg的物块,都以v=4m/s的初速度朝相反方向运动,它们之间有摩擦,薄板足够长,当薄板的速度为2.4m/s时,物块的运动情况是( )| A、做加速运动 | B、做减速运动 | C、做匀速运动 | D、以上运动都可能 |
 如图所示,质量为M,半径为R的光滑半圆弧槽静止在光滑水平面上,有一质量为m的小滑块在与圆心等高处无初速度滑下,在小滑块滑到圆弧槽最低点的过程中,圆弧槽产生的位移的大小为( )
如图所示,质量为M,半径为R的光滑半圆弧槽静止在光滑水平面上,有一质量为m的小滑块在与圆心等高处无初速度滑下,在小滑块滑到圆弧槽最低点的过程中,圆弧槽产生的位移的大小为( ) 如图所示,在光滑水平面上,有一辆质量为M的小车,小车的水平上表面放有一质量为m木块,木块与小车间的动摩擦因数为μ,当用一个大小为F的水平恒力拉小车时,小车带着木块保持相对静止而一起向左加速运动.则在运动过程中( )
如图所示,在光滑水平面上,有一辆质量为M的小车,小车的水平上表面放有一质量为m木块,木块与小车间的动摩擦因数为μ,当用一个大小为F的水平恒力拉小车时,小车带着木块保持相对静止而一起向左加速运动.则在运动过程中( ) 如图所示,一个带有1/4圆弧的粗糙滑板A,总质量为mA=3kg,其圆弧部分与水平部分相切于P,水平部分PQ长为L=3.75m.开始时A静止在光滑水平面上,有一质量为mB=2kg的小木块B从滑板A的右端以水平初速度v0=5m/s滑上A,小木块B与滑板A之间的动摩擦因数为μ=0.15,小木块B滑到滑板A的左端并沿着圆弧部分上滑一段弧长后返回最终停止在滑板A上.
如图所示,一个带有1/4圆弧的粗糙滑板A,总质量为mA=3kg,其圆弧部分与水平部分相切于P,水平部分PQ长为L=3.75m.开始时A静止在光滑水平面上,有一质量为mB=2kg的小木块B从滑板A的右端以水平初速度v0=5m/s滑上A,小木块B与滑板A之间的动摩擦因数为μ=0.15,小木块B滑到滑板A的左端并沿着圆弧部分上滑一段弧长后返回最终停止在滑板A上. 在光滑水平面上放有一根平直的弹性轻质长绳,绳上从左向右均匀分布有一系列质点1,2,3,…,相邻两个质点间的距离均为0.10m.在t=0时刻质点1开始沿垂直于绳的方向在水平面内做简谐运动,运动图象如图所示.此振动沿绳向右传播,当振动刚好传播到质点13时,质点1恰好完成第一次全振动.则( )
在光滑水平面上放有一根平直的弹性轻质长绳,绳上从左向右均匀分布有一系列质点1,2,3,…,相邻两个质点间的距离均为0.10m.在t=0时刻质点1开始沿垂直于绳的方向在水平面内做简谐运动,运动图象如图所示.此振动沿绳向右传播,当振动刚好传播到质点13时,质点1恰好完成第一次全振动.则( )