题目内容
（10分）如图所示，在倾角为37°的斜面两端，垂直于斜面方向固定两个弹性板，两板相距2m，质量为10g，带电量为+1×10－7C的物体与斜面间的动摩擦因数为0.2，物体从斜面中点以大小为10m/s的速度沿斜面开始运动。若物体与弹性板碰撞过程中机械能不损失，电量也不变，匀强电场（方向与斜面平行）的场强E=2×106N/C，求物体在斜面上运动的总路程。（g取10m/s2）
【答案】
40m。
【解析】分析和解答：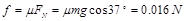
，mgsin37°=0.06N，Eq=0.2N，f+ mgsin37°<Eq，故最后应停在紧靠上边弹性板处，由动能定理得：
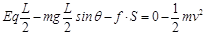，解得：S=40m。
本题考查动能定理的应用，由于重力沿斜面向下的分力和摩擦力的合力小于电场力，可判断物体最后应停在紧靠上边弹性板处，由动能定理（重力、摩擦力、电场力做功）可求得路程大小，要注意重力和电场力做功只与初末位置有关，而摩擦力做功与路程（路径）有关
练习册系列答案
相关题目
如图所示，在倾角为θ=30°的斜面上，固定一宽L=0.25m的平行金属导轨，在导轨上端接入电源和变阻器．电源电动势E=12V，内阻r=1.0Ω一质量m=20g的金属棒ab与两导轨垂直并接触良好．整个装置处于磁感强度B=0.80T、垂直于斜面向上的匀强磁场中（导轨与金属棒的电阻不计）．金属导轨是光滑的，取g=10m/s2，要保持金属棒在导轨上静止，求：
如图所示，在倾角为θ的光滑固定斜面上，劲度系数分别为k1、k2的两个轻弹簧平行于斜面悬挂着，k1在上 k2在下，两弹簧之间有一质量为m1的重物，现用力F（未知）沿斜面向上缓慢推动m2，当两弹簧的总长等于两弹簧的原长之和时，
如图所示，在倾角为30°的斜面上，放置两条宽L=0.5m的平行导轨，将电源、滑动变阻器用导线连接在导轨上，在导轨上横放一根质量m=0.2kg的金属杆ab，电源电动势E=12V，内阻r=0.3Ω，金属杆与导轨间最大静摩擦力为fm=0.6N，磁场方向垂直轨道所在平面，B=0.8T．金属杆ab的电阻为0.2Ω，导轨电阻不计．欲使杆的轨道上保持静止，滑动变阻器的电阻的取值范围多大？（g取10m/s2）
如图所示，在倾角为30°的斜面上，由A点水平抛出一个物体，落在斜面上的B点处，A与B两点间距离是10m，（ 取g=10m/s2）求：
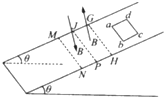如图所示，在倾角为θ的光滑斜面上，存在着两个大小相等、方向相反的匀强磁场，磁场方向与斜面垂直，两磁场的宽度MJ和JG均为L，一个质量为m、电阻为R、边长也为L的正方形导线框，由静止开始沿斜面下滑，当ab边刚越过GH进入磁场时，线框恰好以速度v0做匀速直线运动；当ab边下滑到JP与MN的中间位置时，线框又恰好以速度v做匀速直线运动．则下列说法正确的是（ ）| A、v=v0 | ||
| B、线框离开MN的过程中电流方向为adcba | ||
| C、当ab边刚越过JP时，线框加速度的大小为3 gsinθ | ||
D、从ab边刚越过GH到ab边刚越过MN过程中，线框产生的热量为2mgLsinθ+
|