��Ŀ����
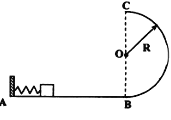
����Ŀ����ͼ��ʾ��һ�����Ǹտ�ʼ�ڰ볤��Ϊa����Բ����˶�������������ΪT�����ص�Q���������Բ�����δ���������У����������ھ���Զ�ص�Pʱͨ��������Բ�������֪����뾶ΪR����������ΪG�������������Ϣ��֪��������
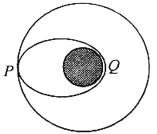
A.������Բ����Ļ�������Ϊ![]()
B.���������Ϊ![]()
C.��������Բ������˶�����Q��ʱ���ٶȴ��ڵ�һ�����ٶ�
D.���Ƿֱ���Բ��������к�����Բ���������ʱ������P��ʱ�ļ��ٶȲ�ͬ
���𰸡�ABC
��������
A�����ݿ����յ��������ɵ�
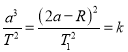
���
![]()
��A��ȷ��
B����
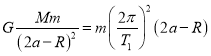
���
![]()
��B��ȷ��
C����һ�����ٶ��ǽ��������ǵ������ٶȣ�Ҳ��������ٶȡ����������ڽ���Բ�������Բ���˶���Q����ٶȵ��ڵ�һ�����ٶȣ��������˶�����Բ������ٶ�������������Բ������˶�����Q��ʱ���ٶȴ��ڵ�һ�����ٶȣ���C��ȷ��
D����
![]()
��֪��ͬһ��Ĺ���뾶��ͬ�������ٶ���ͬ����D����
��ѡABC��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ