题目内容
【题目】如图所示,两块平行金属板竖直放置,两板间的电势差U=1.5×103V(仅在两板间有电场),现将一质量m=1×10﹣2kg、电荷量q=4×10﹣5C的带电小球从两板的左上方距两板上端的高度h=20cm的地方以初速度v0=4m/s水平抛出,小球恰好从左板的上边缘进入电场,在两板间沿直线运动,从右板的下边缘飞出电场,求: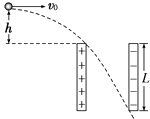
(1)金属板的长度L.
(2)小球飞出电场时的动能Ek .
【答案】
(1)解:小球未进电场前做平抛运动,则小球到达左板上边缘时的竖直分速度: ![]()
设小球此时速度方向与竖直方向之间的夹角为θ,则: ![]()
小球在电场中沿直线运动,所受合力方向与运动方向相同,设板间距为d,
则:tanθ= ![]()
L= ![]()
答:金属板的长度L=0.15m.
(2)解:根据动能定理得:
进入电场前:mgh= ![]()
电场中运动过程: ![]()
解得 Ek=0.175J
答:小球飞出电场时的动能Ek=0.175J.
【解析】(1)平抛运动可以将曲线运动分解成直线运动,利用速度的夹角公式求解。
(2)求动能可以利用两次动能定理 ,一次在进入电场之前,一次为进入电场之后可求解。
【考点精析】通过灵活运用平抛运动和动能定理的理解,掌握特点:①具有水平方向的初速度;②只受重力作用,是加速度为重力加速度g的匀变速曲线运动;运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动;动能定理的表达式是在物体受恒力作用且做直线运动的情况下得出的.但它也适用于变力及物体作曲线运动的情况;功和动能都是标量,不能利用矢量法则分解,故动能定理无分量式即可以解答此题.

练习册系列答案
相关题目