题目内容
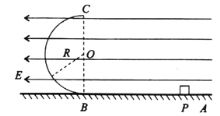
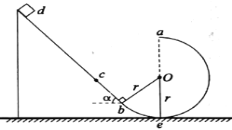
【题目】如图所示，倾角为θ＝45°的光滑平直导轨db与半径为r的光滑圆环轨道相切，切点为b，整个轨道处在竖直平面内。一质力为m的小滑块从导轨上的d处无初速下滑进入圆环轨道，接着小滑块从圆环最高点a水平飞出，恰好击中导轨上与圆心O等高的c点，已知圆环最低点为e点，重力加速度为g，不计空气阻力。求：
（1）小滑块在a点飞出时具有的动能；
（2）小滑块在e点对圆环轨道压力的大小。
【答案】（1）
；（2）6mg
【解析】
（1）小滑块从a点飞出后做平抛运动:
水平方向：
竖直方向：
解得：
va=
小滑块在a点飞出时具有的动能：
（2）小滑块在e点时速度为vm，由机械能守恒定律得：
在最低点由牛顿第二定律:
由牛顿第三定律得：
F′= F
解得：
F′= 6mg；
练习册系列答案
考前必练系列答案
相关题目
