��Ŀ����
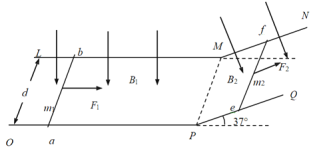
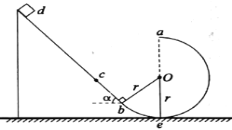
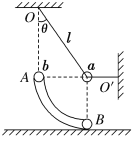
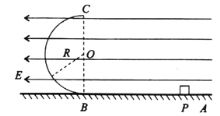
����Ŀ����ͼ��ʾ����ΪR��0.4m��Բ�ξ�Ե�⻬���BC��ˮƽ��Ե�ֲڵĹ��AB��B��ƽ�����ӣ����AB�Ϸ��е糡ǿ�ȴ�СΪE��1.O��104N/C�������������ǿ�糡������һ����m��0.1kg�������q����1.0��10-4C�Ĵ�����(����Ϊ�ʵ�)����ˮƽ����ϵ�P���ɾ�ֹ�ͷţ���������ǡ�ÿ�����Բ������˶���C�㣬�����뿪C�����ص�ˮƽ���ϵ�D��(ͼ��δ����)���������ٶ�g��10m/s2����
��1���������˶���Բ�ι��B��ʱ�Թ����ѹ����С��
��2����������ص�ˮƽ���ϵ�D�㵽B��ľ��룻
��3��������ӿ�ʼ�˶�����ص�ˮƽ�����������е������(���������λ��Ч����)��
���𰸡���1��6.0N ����2��0 ����3��1.17J��![]() JҲ�ԣ�
JҲ�ԣ�
��������
��1���������ͨ��C��ʱ���ٶ�ΪvC������ţ�ٵڶ�������
mg=m![]()
���
vC=2.0m/s
�������ͨ��B��ʱ���ٶ�ΪvB�������Դ������֧������СΪFB����������B��ʱ������ţ�ٵڶ������У�
![]() ��
��
�������B�˶���C�Ĺ����У����ݶ��ܶ����У�
![]()
�������
FB=6.0N��
����ţ�ٵ������ɣ�������Թ����ѹ��
F��B=6.0N��
��2������������ߵ�C����ˮƽ����ϵ�D�㾭����ʱ��Ϊt�������˶��ķֽ��У�
2R=![]() ��
��
![]() ��
��
�������
![]() ��
��
��3����P�㵽B��������������˶���������ٶ�һ�������ڴ�B��C�Ĺ����У��ڴ˹�����ֻ�������͵糡������������������С��ȣ�����������������45���н�б�����·���������ٶȱس�����B���Ҳ��ӦԲ�Ľ�Ϊ45������
�������������ΪEkm�����ݶ��ܶ����У�
qERsin45��-mgR��1��cos45����=Ekm-![]()
�������ݽ��
Ekm��1.17J��![]() JҲ�ԣ�
JҲ�ԣ�

 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д� ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�