题目内容
1.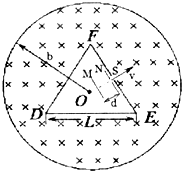 如图所示,在半径为b(大小未知)的圆形区域内,固定放置一绝缘材料制成的边长为L的弹性等边三角形框架DEF,其中心O位于磁场区域的圆心.在三角形框架DEF与圆周之间的空间中,充满磁感应强度大小为B的均匀磁场,其方向垂直纸而向里.在三角形DEF内放置平行板电容器MN,两板间距为d,N板紧靠EF边,N板及EF中点S处均开有小孔,在两板间靠近M板处有一质量为m,电量为q (q>0)的带电粒子由静止释放,粒子经过S处的速度大小为v=$\frac{qBL}{2m}$,方向垂直于EF边并指向磁场.若粒子与三角形框架的碰撞均为弹性碰撞,且粒子在碰撞过程中质量、电量均不变,不计带电粒子的重力,平行板电容器MN产生的电场仅限于两板间,求:
如图所示,在半径为b(大小未知)的圆形区域内,固定放置一绝缘材料制成的边长为L的弹性等边三角形框架DEF,其中心O位于磁场区域的圆心.在三角形框架DEF与圆周之间的空间中,充满磁感应强度大小为B的均匀磁场,其方向垂直纸而向里.在三角形DEF内放置平行板电容器MN,两板间距为d,N板紧靠EF边,N板及EF中点S处均开有小孔,在两板间靠近M板处有一质量为m,电量为q (q>0)的带电粒子由静止释放,粒子经过S处的速度大小为v=$\frac{qBL}{2m}$,方向垂直于EF边并指向磁场.若粒子与三角形框架的碰撞均为弹性碰撞,且粒子在碰撞过程中质量、电量均不变,不计带电粒子的重力,平行板电容器MN产生的电场仅限于两板间,求:(1)MN间匀强电场的场强大小;
(2)若从S点发射出的粒子能再次返回S点,则圆形区域的半径b至少为多大?
(3)若圆形区域的半径b满足第(2)问的条件,则从M板处出发的带电粒子第一次返回M板处的时间是多少.
分析 (1)带电粒子在匀强电场中做匀加速直线运动,由动能定理求出MN间匀强电场的场强大小;
(2)带电粒子在匀强磁场中,只受洛伦兹力作用,由洛伦兹力提供向心做匀速圆周运动,画出运动的轨迹图,由结合几何关系和圆周运动规律,求出圆形区域的半径b的最小值;
(3)根据带电粒子在磁场中做匀速圆周运动的轨迹图,找到圆周运动的圆心角,结合圆周运动周期公式,求出在磁场中运动的时间;带电粒子在电场中做匀加速直线运动,根据匀加速直线运动的规律,求出在电场中运动的时间,两个时间相加得出运动的总时间.
解答 解:(1)带电粒子在匀强电场中做匀加速直线运动,
由动能定理:$Eqd=\frac{1}{2}m{v}^{2}$
得:$E=\frac{{qB}^{2}{L}^{2}}{8dm}$;
(2)带电粒子在匀强磁场中做匀速圆周运动,运动轨迹如图,
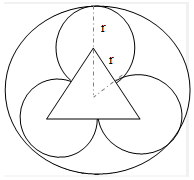
由洛伦兹力提供向心力:$qvB=m\frac{{v}^{2}}{r}$
$r=\frac{mv}{qB}=\frac{L}{2}$
粒子运动轨迹与磁场圆内切时磁场圆半径最小,
由几何关系得:
${b}_{min}=r+\frac{\sqrt{3}}{3}L=(\frac{1}{2}+\frac{\sqrt{3}}{3})L$
(3)粒子在磁场中做匀速圆周运动的周期:$T=\frac{2πr}{v}=\frac{2πm}{qB}$,
由运动轨迹知粒子在磁场中重复运动三次,圆心角为300°,
粒子在磁场中运动的总时间:${t}_{1}=3×\frac{300°}{360°}T=3×\frac{5}{6}T=\frac{5πm}{qB}$,
带电粒子在匀强电场中做匀加速直线运动,由M到N和N到M的时间相等,
粒子在电场中运动的平均速度:$\overline{v}=\frac{v}{2}$,
粒子在电场中运动的总时间:${t}_{2}=2×\frac{d}{\overline{v}}=\frac{8md}{BqL}$,
则粒子运动一周的总时间:$t={t}_{1}+{t}_{2}=\frac{5πm}{qB}+\frac{8md}{qBL}$,
答:(1)MN间匀强电场的场强大小为$E=\frac{{qB}^{2}{L}^{2}}{8dm}$;
(2)圆形区域的半径b的最小值为${b}_{min}=(\frac{1}{2}+\frac{\sqrt{3}}{3})L$;
(3)粒子从M板处出发的带电粒子第一次返回M板处的时间是$t=\frac{5πm}{qB}+\frac{8md}{qBL}$.
点评 本题是带电粒子在复合场中的周期性运动问题,综合性较强,熟练应用动能定理和牛顿运动定律是解决带电粒子在匀强电场中运动的关键;而画出运动轨迹,找几何关系结合洛伦兹力提供向心力立方程,则是解决带电粒子在匀强磁场中运动的关键;第三问要求第一次返回到M板的时间,读题过程容易理解成第一次回到S点的时间,是一个易错点.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案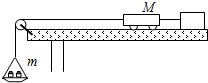 如图所示是某同学探究加速度与力、质量关系的实验装置.将一辆小车放在光滑的水平板上,小车前端系上细绳,绳的另一端跨过定滑轮挂一小盘,盘里放适量的砝码,盘与砝码的总质量为m,车后端连一纸带,穿过打点计时器限位孔,小车运动时带动纸带运动,通过打点计时器记录下小车运动的情况.该同学通过在小车上加减砝码改变小车的质量M,通过在盘中增减砝码改变小车所受的合力F,研究纸带算出小车运动的加速度a,几次实验数据记录如下表:
如图所示是某同学探究加速度与力、质量关系的实验装置.将一辆小车放在光滑的水平板上,小车前端系上细绳,绳的另一端跨过定滑轮挂一小盘,盘里放适量的砝码,盘与砝码的总质量为m,车后端连一纸带,穿过打点计时器限位孔,小车运动时带动纸带运动,通过打点计时器记录下小车运动的情况.该同学通过在小车上加减砝码改变小车的质量M,通过在盘中增减砝码改变小车所受的合力F,研究纸带算出小车运动的加速度a,几次实验数据记录如下表:| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| M/kg | 1.00 | 1.00 | 1.00 | 1.00 | 1.25 | 1.50 | 2.00 | 2.50 |
| F/N | 0.25 | 0.50 | 0.75 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| a/(m•s-2) | 0.25 | 0.51 | 0.74 | 0.99 | 0.80 | 0.67 | 0.50 | 0.40 |
(2)在实验中为了探究小车的加速度与力和质量的关系,该同学采用了先保持小车质量M不变,研究另两个量间的关系,这种方法叫做控制变量法;
(3)通过表中1-4列数据可得到的结论是:当小车质量不变时,小车的加速度与合外力成正比;
通过表中4-8列数据可得到的结论是:当小车受到的合外力不变时,小车的加速度与质量成反比.
| 序号 | 器材 | 说明 |
| ① | 金属丝(L) | 长度为L0,直径为D,阻值约10Ω |
| ② | 电流表(A1) | 量程10mA,内阻r1=30Ω |
| ③ | 电流表(A2) | 量程500μA 内阻r2=800Ω |
| ④ | 电压表V | 量程为10V,内阻为10kΩ |
| ⑤ | 电阻(R1) | 阻值为100Ω,起保护作用 |
| ⑥ | 滑动变阻器(R2) | 总阻值约10Ω |
| ⑦ | 电源(E) | 电动势1.5V,内阻很小 |
| ⑧ | 开关(S) | |
| ⑨ | 导线若干 |
(2)若实验要求方法简捷,有尽可能高的测量精度,并能得到多组数据,实验应选择的器材为①②③⑤⑥⑦⑧⑨(填写序号),请在图2方框中画出你所设计的实验电路图.

 一定质量理想气体在初始状态A时,压强PA=1×105Pa,结合如图(V-T图线)中交代的信息,试求:
一定质量理想气体在初始状态A时,压强PA=1×105Pa,结合如图(V-T图线)中交代的信息,试求: