题目内容
【题目】如图，平行金属板水平放置，一带电荷量为q（q＞0）、质量为m的a粒子从板的左侧O点沿两板间的中线以初速度v0射入板间，结果粒子恰好从上板的右侧边缘与静止在此处的另一不带电、等质量的b粒子碰后粘在一起，进入一圆形有界匀强磁场，磁场方向垂直于纸面，圆形磁场的圆心与上板在同一直线上．两粒子经磁场偏转后射出磁场，沿水平方向返回两板间，它们又刚好返回到O点．不计粒子重力，金属板长为L，板上所加电压为U= 
，求：
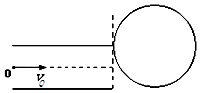
（1）a粒子刚出电场时的速度大小；
（2）两粒子从板右端返回电场时的位置与下板间的距离；
（3）a粒子在磁场运动过程中所受洛仑兹力大小和洛仑兹力对a粒子的冲量．
【答案】
（1）解：设所求为v，由动能定理有：
qU= mv2﹣ mv02
可得 v= 
答：a粒子刚出电场时的速度大小为 ．
（2）a粒子在电场中水平方向匀速，得 
，由上知出电场时竖直方向vy=v0
则有y1= vyt1= L，所以两板距离为L
返回时，两粒子在电场中仍做类平抛运动，刚好到O点，
则有 
， 
．
则进入电场的位置与下板的间距为 
答：两粒子从板右端返回电场时的位置与下板间的距离为0．
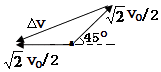
（3）由图知，θ=450，由几何关系知 
得 
而两粒子碰撞，由动量守恒有mv=2mv1，得v1= 
所求f洛=2 
= 
由动量定理知：I洛=2m△v，如图可得△v= 
则I洛= 
，方向斜下左下方与水平方向成22.5°．
答：a粒子在磁场运动过程中所受洛仑兹力大小为 、洛仑兹力对a粒子的冲量为 ，方向斜下左下方与水平方向成22.5°．
【解析】（1）运动过程中只有电场力做功，利用动能定理直接列式求解。
（2）粘在一起的两粒子在磁场中做匀速圆周运动后，穿出磁场后沿水平方向进入电场，又刚好回到O点，这样两粒子共同在电场中做类平抛运动，由初速度、加速度、位移，就能求出竖直位移，从而能求出返回电场时的位置与下板的距离．
（3）a粒子受到的洛仑兹力提供给两粒子一起做匀速圆周运动，则a粒子受到洛仑兹力就是两粒子做匀速圆周运动的向心力，由几何关系求出两粒子做匀速圆周运动的半径，从而可以求得向心力也就是a粒子的洛仑兹力；至于洛仑兹力对a粒子的冲量，可以由动量定理来求，但要注意的是动量变化是矢量差．
