题目内容
10.某校A、B两个兴趣小组想探究铅笔芯(圆柱形)的电阻率,他们各自选取 一段长为L的粗细均匀的锐笔芯,根据所学知识设计了不同的方案进行实验:
(1)先用游标卡尺测量铅笔芯的直径d,某次测量如图(甲)所示,其读数为2.5mm
(2)A组方案:实验电路如图(乙)所示(整根铅笔芯连在电路中).根据实验测出的多 组数据在坐标纸上描点,如图(丙)所示,请在答题纸相应位置的图中完成该铅笔 芯的U-I图线,并裉据图线求出其电阻值R=5Ω再由阻值可求得其电阻率.
(3)B组方案:实验电路如图(丁)所示.主要步骤如下,请完成相关问题:

a.闭合开关单刀双掷开关S2扳到“1”位置,调节变阻器R′,使电压表为某一 适当的读数,测景并记下金属滑环到铅笔芯左端0点的距离L;
b.保持R′不变,开关S2扳到“2”位置,调节电阻箱阻值如图(戊)所示,电压表的 读数与开关S2位于“1”位置时相同,则这段长度为L的铅笔芯的电阻值为2.2Ω.
C.移动金属滑环,重复a、b步骤.记下多组R、L数据,并画出R-L图线.
若图线的斜率为k则求出该铅笔芯的电阻率为$\frac{kπ{d}^{2}}{4L}$ (结果用k、L、d、π表示)
(4)从电压表内阻对实验结果的影响考虑,较合理的方案是B组(填“A”或“B”).
分析 (1)游标卡尺读数的方法是主尺读数加上游标读数,不需估读.
(2)用一条过坐标原点的直线将各个点连接起来,直线的斜率表示电阻;
(3)电阻箱各旋盘对应的指示点的示数乘以面板上标记的倍数,然后加在一起,就是接入电路的电阻值.
(4)从减小误差的角度分析.
解答 解:(1)游标卡尺的主尺读数为2mm,游标读数为0.1×5mm=2.5mm,所以最终读数为2.5mm.
(2)如图,用一条过坐标原点的直线将各个点连接起来,直线的斜率表示电阻
根据欧姆定律,电阻为R=$\frac{3}{0.6}$Ω=5Ω
(3).电阻箱各旋盘对应的指示点的示数乘以面板上标记的倍数,然后加在一起,就是接入电路的电阻值,故R=2.2Ω
根据电阻定律,可得ρ=$\frac{kS}{L}$=$\frac{kπ{d}^{2}}{4L}$.
(4)方案A中,由于电压表的分流作用,电流测量值偏大,故电阻测量值偏小,而方案B中电阻测量值较为准确;
故答案为:(1)2.5;(2)5;(3)2.2,$\frac{kπ{d}^{2}}{4L}$;(4)B.
点评 解决本题的关键掌握游标卡尺和螺旋测微器的读数方法,游标卡尺读数的方法是主尺读数加上游标读数,不需估读.
本题是用伏安法测电阻和用替代法测电阻,关键要明确误差的来源,能根据图象求出电阻值.同时要熟悉电阻箱的读数.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
1. 如图所示.在竖直方向不同的高度a、b两点,同时水平抛出两个小球,高度之比为ha:hb=1:4,水平射程sa:sb=2:1,两球从抛出到落地的时间分别为ta,tb,则下列判断正确的是( )
如图所示.在竖直方向不同的高度a、b两点,同时水平抛出两个小球,高度之比为ha:hb=1:4,水平射程sa:sb=2:1,两球从抛出到落地的时间分别为ta,tb,则下列判断正确的是( )
 如图所示.在竖直方向不同的高度a、b两点,同时水平抛出两个小球,高度之比为ha:hb=1:4,水平射程sa:sb=2:1,两球从抛出到落地的时间分别为ta,tb,则下列判断正确的是( )
如图所示.在竖直方向不同的高度a、b两点,同时水平抛出两个小球,高度之比为ha:hb=1:4,水平射程sa:sb=2:1,两球从抛出到落地的时间分别为ta,tb,则下列判断正确的是( )| A. | c点是两球在空中相碰点 | B. | Va:Vb=2:1 | ||
| C. | ta:tb=1:2 | D. | 两球落地速度可能相等 |
5.阅读如下资料,并根据资料中有关信息回答问题:
(1)由于两个物体相对位置的变化引起的引力场的能量变化(与某一零位置相比).称作为这一对物体的引力势能,则万有引力势能可由此式算:EP=-$\frac{GMm}{r}$(设无穷远处Ep=0)式中M、m分别代表两个物体的质量,r物体中心距离,G为万有引力常量.
(2)处于某一星体表面的物体只要有足够大的速度就能够摆脱该星体的引力飞到无穷远,这一速度就叫做星体的逃逸速度.
(3)大约200年前法国数学家兼天文学家拉普拉斯曾预言一个密度跟地球相同,直径为太阳250倍的发光星体,由于其引力作用将不允许任何光线离开它,其逃逸速度大于真空中的光速,这一奇怪的黑体就叫做黑洞.
(4)以下是太阳的有关数据.在下列问题中,把星体(包括黑洞)看做是一个质量分布均匀的球体.
①如果地球的质量为M地,半径为R地,试计算地球的逃逸速度;若物体绕地球表面做匀速圆周运动的速度为7.9km/s,则物体摆脱地球引力的逃逸速度为多大?
②试估算太阳表面的重力加速度与地球表面的重力加速度的比值.
③已知某星体演变为黑洞时质量为M,求该星体演变为黑洞时的临界半径rg
④若太阳最终可以演变为黑洞,则它演变为黑洞时的临界半径rg为多少米?
(1)由于两个物体相对位置的变化引起的引力场的能量变化(与某一零位置相比).称作为这一对物体的引力势能,则万有引力势能可由此式算:EP=-$\frac{GMm}{r}$(设无穷远处Ep=0)式中M、m分别代表两个物体的质量,r物体中心距离,G为万有引力常量.
(2)处于某一星体表面的物体只要有足够大的速度就能够摆脱该星体的引力飞到无穷远,这一速度就叫做星体的逃逸速度.
(3)大约200年前法国数学家兼天文学家拉普拉斯曾预言一个密度跟地球相同,直径为太阳250倍的发光星体,由于其引力作用将不允许任何光线离开它,其逃逸速度大于真空中的光速,这一奇怪的黑体就叫做黑洞.
(4)以下是太阳的有关数据.在下列问题中,把星体(包括黑洞)看做是一个质量分布均匀的球体.
| 太阳的半径 | R日=7×105km=110R地球 |
| 太阳的质量 | M日=2×1030kg=3.33×105M地球 |
| 平均密度 | ρ日=1.4×103kg/m3=$\frac{1}{4}$ρ地球 |
| 自传周期 | 赤道附近26天,两极附近长于30天 |
②试估算太阳表面的重力加速度与地球表面的重力加速度的比值.
③已知某星体演变为黑洞时质量为M,求该星体演变为黑洞时的临界半径rg
④若太阳最终可以演变为黑洞,则它演变为黑洞时的临界半径rg为多少米?
2. 如图所示的电路中,R1、R2均为定值电阻,R3为可变电阻,电源的电动势为E,内阻为r.A为内阻可忽略的电流表,V为内阻很大的电压表,当R3滑动触头向图中a端移动时( )
如图所示的电路中,R1、R2均为定值电阻,R3为可变电阻,电源的电动势为E,内阻为r.A为内阻可忽略的电流表,V为内阻很大的电压表,当R3滑动触头向图中a端移动时( )
 如图所示的电路中,R1、R2均为定值电阻,R3为可变电阻,电源的电动势为E,内阻为r.A为内阻可忽略的电流表,V为内阻很大的电压表,当R3滑动触头向图中a端移动时( )
如图所示的电路中,R1、R2均为定值电阻,R3为可变电阻,电源的电动势为E,内阻为r.A为内阻可忽略的电流表,V为内阻很大的电压表,当R3滑动触头向图中a端移动时( )| A. | 电压表V的读数变小 | B. | 电压表V的读数变大 | ||
| C. | 电流表A的读数变小 | D. | 电流表A的读数变大 |
19. 如图,用等长的绝缘线悬挂着两个带同种电荷的小球,电量分别为q1、q2;质量分别为m1、m2.静止时α>β,造成α>β的原因是( )
如图,用等长的绝缘线悬挂着两个带同种电荷的小球,电量分别为q1、q2;质量分别为m1、m2.静止时α>β,造成α>β的原因是( )
 如图,用等长的绝缘线悬挂着两个带同种电荷的小球,电量分别为q1、q2;质量分别为m1、m2.静止时α>β,造成α>β的原因是( )
如图,用等长的绝缘线悬挂着两个带同种电荷的小球,电量分别为q1、q2;质量分别为m1、m2.静止时α>β,造成α>β的原因是( )| A. | m1<m2 | B. | m1>m2 | C. | q1>q2 | D. | q1<q2 |
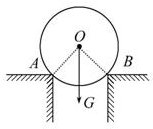
 如图所示,一重量为100N的物体,由OA、OB两条细绳悬挂在两边的墙壁上而处于静止状态,已知OA绳子处于水平状态,OB与水平方向夹角为60度,则两细绳上拉力大小是否相同?如果不同,谁的拉力大,大多少?
如图所示,一重量为100N的物体,由OA、OB两条细绳悬挂在两边的墙壁上而处于静止状态,已知OA绳子处于水平状态,OB与水平方向夹角为60度,则两细绳上拉力大小是否相同?如果不同,谁的拉力大,大多少?