Question

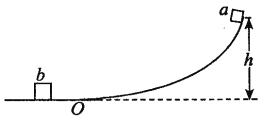
【题目】如图所示，竖直放置的半圆形光滑绝缘轨道半径为R，圆心为O．下端与绝缘水平轨道在B点平滑连接，一质量为m带正电的物块（可视为质点），置于水平轨道上的A点。已如A、B两点间的距离为L，物块与水平轨道间的动摩擦因数为μ，重力加速度为g。

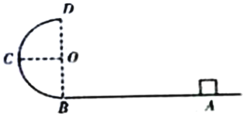
(1)若物块能到达的最高点是半圆形轨道上与圆心O等高的C点，则物块在A点水平向左运动的初速度应为多大?

(2)若在整个空同加上水平向左的匀强电场，场强大小为E= (q为物块的带电量)，现将物块从A点由静止释放，且运动过程中始终不脱离轨道，求物块第2次经过B点时的速度大小。

(3)在(2)的情景下，求物块第2n(n=1，2、3……)次经过B点时的速度大小。

Answer 1

【答案】(1) (2) (3) ，其中n＝1、2、3…….

【解析】

(1)设物块在A点的速度为v1，由动能定理有

－μmgL－mgR＝0－m

解得 v1＝

(2)对物块由释放至第一次到B点过程中，其经过B点速度为所求

知：()L＝m

可得：

(3)设第2、4、6、…、2n次经过B点时的速度分别为v2、v4、…、v2n，

第2、4、6、…、2(n－1)次离开B点向右滑行的最大距离分别为L1、L2、…、Ln－1，

则：－()L1＝0－m

()L1＝m

解得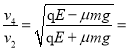

同理＝ ……＝

综上可得

v2n＝ 其中 n＝1、2、3…