��Ŀ����
����Ŀ����ͼ��ʾ���⻬�Ĺ���̶�����ֱƽ���ڣ���O�����Ϊˮƽ�����O���ұߵ��������߶�h��0.45m���������ι����O��ƽ�����ӡ�����m��0.10kg��С����a�ɾ�ֹ��ʼ���������Ķ����ع���»�������ˮƽ�κ��봦�ھ�ֹ״̬������M��0.30kg��С����b������ײ����ײ��С����aǡ��ֹͣ�˶���ȡ�������ٶ�g��10m/s2����
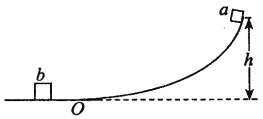
��1��С����aͨ��O��ʱ���ٶȴ�С��
��2����ײ��С����b���ٶȴ�С
��3����ײ������С����a��b��ɵ�ϵͳ��ʧ�Ļ�е�ܡ�
���𰸡���1��3m/s����2��1m/s����3��0.3J��
��������
��1��С��������߹�����»��Ĺ����У�
�ɻ�е���غ㶨�ɵã�![]()
�������ݽ�ã�С����aͨ��O��ʱ���ٶȣ�v0��3m/s��
��2����ײ����ϵͳ�����غ㣬������Ϊ������
�ɶ����غ㶨�ɵã�mv0��Mv1��
�������ݽ�� v1��1m/s��
��3����ײ������С����a��b��ɵ�ϵͳ��ʧ�Ļ�е�ܣ���E��![]() mv02��
mv02��![]() Mv12��
Mv12��
�������ݽ����E��0.3J

��ϰ��ϵ�д�
�����Ŀ