题目内容
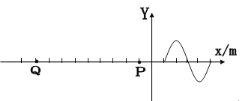
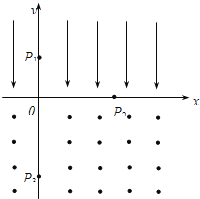
【题目】如图所示，在某一真空区域，x<0的区域有磁感应强度为B1的匀强磁场，x>0的区域有磁感应强度为B2的匀强磁场，且
，方向均垂直纸面向里。在t=0时刻，处于坐标原点的一个静止中性粒子（不计重力）裂变为两个带电粒子a和b，质量分别为ma和mb。已知裂变后瞬时，带正电粒子a的速度方向沿x轴正方向。忽略粒子间的相互作用力。求：
（1）裂变后粒子a在匀强磁场B2中的回旋半径与粒子b在匀强磁场B1中的回旋半径之比为多少。
（2）
为何值时，两粒子裂变以后又能在磁场的分界线y轴上相遇。
【答案】(1) 
(2) 当在a点相遇时， 
； 当在b点相遇时， 
；当在c点相遇时， 
【解析】（1）粒子裂变过程系统动量守恒，以向右为正方向，由动量守恒定律得：mava-mbvb=0，
裂变后两粒子的动量大小：P=mv相等，
裂变前粒子是中性粒子，由电荷守恒定律可知，裂变后，粒子的电荷量大小相等，即：qa=qb=q，
粒子在磁场中做圆周运动，洛伦兹力提供向心力，由牛顿第二定律得：qvB=m
练习册系列答案
考前必练系列答案
相关题目
