Question

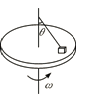
【题目】如图所示，水平转台上有一个质量为m的小物块，用长为L的轻细绳将物块连接在通过转台中心的转轴上，细绳与竖直转轴的夹角为θ，系统静止时细绳绷直但张力为零．物块与转台间动摩擦因数为μ（μ＜tanθ），设最大静摩擦力等于滑动摩擦力．当物块随转台由静止开始缓慢加速转动且未离开转台的过程中

A. 物块受转台的静摩擦力方向始终指向转轴

B. 至绳中出现拉力时，转台对物块做的功为

C. 物块能在转台上随转台一起转动的最大角速度为

D. 细绳对物块拉力的瞬时功率始终为零

Answer 1

【答案】CD

【解析】物体做加速圆周运动，所以开始时物体受到的摩擦力必定有一部分的分力沿轨迹的切线方向，起到加速的作用，故A错误；对物体受力分析知物块离开圆盘前，由摩擦力和拉力的合力提供向心力： ，在竖直方向上：N+Tcosθ=mg，根据动能定理知： ，当弹力T=0，半径为：r=Lsinθ，联立以上解得： ，至绳中出现拉力时，转台对物块做的功为，故B错误；当N=0，f=0时加速度最大，根据牛顿第二定律： ，Tcosθ=mg，半径为：r=Lsinθ，联立可得： ，所以当物块的角速度增大到时，物块与转台间恰好无相互作用，故C正确；根据几何关系可知，物体在做圆周运动的过程中受到的绳子的拉力方向与物体运动的方向始终垂直，所以细绳对物块拉力的瞬时功率始终为零，故D正确。所以CD正确，AB错误。