题目内容
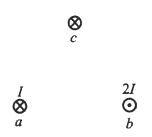
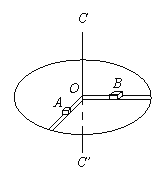
【题目】半径为R的水平圆台,可绕通过圆心O的竖直光滑细轴CC ′ 转动,如图所示,圆台上沿相互垂直的两个半径方向刻有凹槽,质量为mA的物体A放在一个槽内,物体A与槽底间的动摩擦因数为μ,质量为mB的物体B放在另一个槽内,此槽是光滑的.AB间用一长为l(l<R)且不可伸长的轻绳绕过细轴相连.已知圆台做匀速转动,且A、B两物体相对圆台不动(A、B两物体可视为质点,物体的最大静摩擦力近似等于滑动摩擦力).
(1)当圆台转动的角速度为ω0,OA的长度为l1时,试写出A、B两个物体受到的向心力大小的表达式.
(2)不论圆台转动的角速度为多大,要使物体A和槽之间恰好没有摩擦力,则OA的长为多大?
(3)设OA长为x,试分析圆台的角速度ω和物体A到圆心的距离x所应满足的条件.
【答案】
⑴ FA = mAω02l1 …………………………………………………………………1分
FB = mBω02(l – l1) …………………………………………………………………1分
⑵ F = mAω2l1 …………………………………………………………………1分
F = mBω2(l – l1) ……………………………………………………………………1分
解得 ![]() …………………………………………………………1分
…………………………………………………………1分
⑶ 当A、B两物体相对转台静止且恰无摩擦时,物体A、B的动力学方程分别为
F = mAω2x, F = mBω2(l – x),联立解得![]() ……………………1分
……………………1分
当A、B两物体相对转台静止且A恰没有做远离轴心的运动时,物体A、B的动力学方程分别为
F+μmAg=mAω2x,F=mBω2(l-x)
 ,
,![]() …………………………1分
…………………………1分
当A、B两物体相对转台静止且A恰没有做向轴心的运动时,物体A、B的动力学方程分别为
F - μmAg = mAω2x,F = mBω2(l - x)
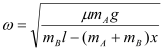 ,
,![]() …………………………1分
…………………………1分
综上分析可知

【解析】略

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案