题目内容
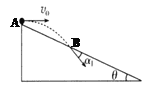
【题目】如图所示,倾角θ=37°的斜面体固定在水平地面上,斜面长L=2.4m.质量M=2.0kg的B物体放在斜面底端,与斜面间的动摩擦因数μ=0.25,通过轻细绳跨过光滑的定滑轮与A物体相连接,连接B的细绳与斜面平行.A的质量m=2.5kg,绳拉直时用手托住A物体使其在距地面h高处由静止释放,着地后立即停止运动. A、B物体均可视为质点,取g=10m/s2,sin37=0.6,cos37=0.8.

(1)求A物体下落的加速度大小及绳子拉力T的大小;
(2)求当A物体从多高处静止释放,B物体恰好运动至斜面最高点;
(3)若A物体从h1=1.6m处静止释放,要使B物体向上运动且不从斜面顶端滑出,求A物体质量m的取值范围.(设B物体受到的最大静摩擦力等于滑动摩擦力)
【答案】(1)20N (2)1.92m (3)![]()
【解析】试题分析:分别对A、B受力分析,结合牛顿第二定律即可求出绳子上的拉力和物体的加速度;根据牛顿第二定律求出速度,A着地后,B沿斜面做匀减速运动,当速度减为零时,根据速度位移公式即可求出B能沿斜面滑行的距离最大时A的高度;根据牛顿第二定律求出A着地后B向上滑行的加速度,由速度位移关系求出相应的位移,在结合力学关系求出相应的质量。
(1)根据牛顿第二运动定律
根据牛顿第二定律对A有:mg-T=ma
根据牛顿第二定律对B有: ![]()
代入数据解得:a=2 m/s2
绳子拉力大小:T=20 N
(2)设物体A着地时B的速度为v,A着地后B做匀减速运动的加速度大小为a1
根据牛顿第二定律对B有: ![]()
代入数据解得:a1= m/s2
对B由运动学公式得:着地前: ![]()
着地后: ![]()
代入数据解得:h=1.92 m
(3)设A着地后B向上滑行距离x
由运动学公式得: ![]()
位移关系满足: ![]()
着地前: ![]()
代入数据解得: ![]()
另一方面要能拉动必须有: ![]()
解得: ![]()
所以物体A的质量范围是: ![]()

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案