题目内容
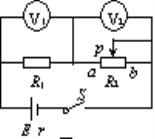
【题目】在倾角θ=30°的斜面上,固定一金属框,宽l=0.25 m,接入电动势E=12 V、内阻不计的电池.垂直框面放置一根质量m=0.2 kg的金属棒ab,它与框架间的动摩擦因数μ=![]() ,整个装置放在磁感应强度B=0.8 T、垂直框面向上的匀强磁场中,如图所示.当调节滑动变阻器R的阻值在什么范围内时,可使金属棒静止在框架上?(框架与金属棒的电阻不计,g取10 m/s2)
,整个装置放在磁感应强度B=0.8 T、垂直框面向上的匀强磁场中,如图所示.当调节滑动变阻器R的阻值在什么范围内时,可使金属棒静止在框架上?(框架与金属棒的电阻不计,g取10 m/s2)

【答案】1.4 Ω--8.0 Ω
【解析】试题分析:根据左手定则可得安培力的方向沿斜面向上,当安培力过大时,则棒有上滑趋势,则静摩擦力沿斜面向下;当安培力过小时,则棒有下滑的趋势,则静摩擦力沿斜面向上,根据力的平衡条件可求出两种安培力的大小,从而确定滑动变阻器的电阻范围。
(1)当滑动变阻器R取值较大时,I较小,安培力F安较小,金属棒有沿框面下滑的趋势,金属棒所受静摩擦力沿框面向上,如图所示:

此时金属棒刚好不下滑,满足平衡条件:
![]()
此时的电流为: ![]()
带入数据解得: ![]()
(2)当滑动变阻器R取值较小时,I较大,安培力F安较大,会使金属棒产生上滑的趋势,因此金属棒所受静摩擦力沿框面向下,受力如图所示:
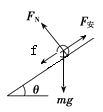
此时金属棒刚好不上滑,满足平衡条件:
![]()
此时的电流为: ![]()
带入数据解得: ![]()
由上可得R的阻值范围为: ![]()

练习册系列答案
相关题目