��Ŀ����
����Ŀ����ͼ����ʾ��A��ԭ����ʱͣ��һˮƽ·���ϣ�B���ں���������A��������A��˾�����ֺ�����A������A��˾������B��Ϊ��ʱ��㣨t=0����A��B������v��tͼ����ͼ����ʾ����֪B���ڵ�1s����A���ľ���������X1=12m��
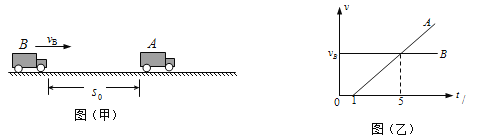
��1����B���˶����ٶ�VB��A���ļ��ٶ�a�Ĵ�С��
��2����S0=30mʱA��B�����Ƿ���ײ����˵�����ɣ�
��3����A��B����������ײ����A��˾������B��ʱ��t=0�������ľ���S0Ӧ����ʲô������
���𰸡���1��12m/s��3m/s2��2����������ײ��3��s0��36m
�����������������B������ֱ���˶�������![]() ����ٶȴ�С������ͼ���б�ʱ�ʾ���ٶ����A�ļ��ٶȴ�С��B���������˶������ٶ���A�����ʱ�����û����A����������������ײ���������ٶ���ȣ�B������A��������������ײ�����������ٶ����ʱλ�ƹ�ϵ���ж������ܷ���ײ���������ٶȴﵽ���ʱ�������ľ���ﵽ��С�������ͼ�������ε�������ɣ�
����ٶȴ�С������ͼ���б�ʱ�ʾ���ٶ����A�ļ��ٶȴ�С��B���������˶������ٶ���A�����ʱ�����û����A����������������ײ���������ٶ���ȣ�B������A��������������ײ�����������ٶ����ʱλ�ƹ�ϵ���ж������ܷ���ײ���������ٶȴﵽ���ʱ�������ľ���ﵽ��С�������ͼ�������ε�������ɣ�
��1����![]() ʱA�����������������̵ľ���Ϊ
ʱA�����������������̵ľ���Ϊ![]() �����
�����![]() ��
��
�ٶ�ͼ���б�ʱ�ʾ���ٶȣ���A���ļ��ٶ�Ϊ![]() ��
��
��2���ٶ����ʱ��B��λ��![]()
A����λ��![]() ��������������ײ��
��������������ײ��
��3���������ٶȴﵽ���ʱ�������ľ���ﵽ��С����Ӧ��v-tͼ���t2=5s����ʱ�����ѷ��������λ��Ϊ���ε����Ϊ![]() ��
��
��ˣ�ҪʹA��B����������ײ������![]() Ӧ��������Ϊ
Ӧ��������Ϊ![]() ��
��








