题目内容
【题目】如图所示,竖直平面内放一直角杆,杆的各部分均光滑,水平部分套有质量为mA=3kg的小球A,竖直部分套有质量为mB=2kg的小球B,A、B之间用不可伸长的轻绳相连。在水平外力F的作用下,系统处于静止状态,且![]() ,重力加速度g=10m/s2。则
,重力加速度g=10m/s2。则
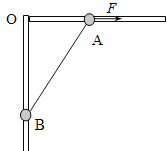
A. 系统平衡时,水平拉力F的大小为25N
B. 系统平衡时,水平杆对小球A弹力的大小为50N
C. 若改变水平力F大小,使小球A由静止开始,向右做加速度大小为4.5m/s2的匀加速直线运动,经过![]() 时小球B的速度大小为4m/s
时小球B的速度大小为4m/s
D. 若改变水平力F大小,使小球A由静止开始,向右做加速度大小为4.5m/s2的匀加速直线运动,经过![]() 的时间内拉力F做的功为49.5J
的时间内拉力F做的功为49.5J
【答案】BCD
【解析】
对AB整体受力分析,受拉力F、重力G、支持力N和向左的弹力N1,根据共点力平衡条件,对整体,竖直方向:N=G1+G2;水平方向:F=N1;解得:N=(m1+m2)g=50N,对小球B:![]() ,则F=15N,故A错误,B正确。若改变水平力F大小,使小球A由静止开始,向右做加速度大小为4.5m/s2的匀加速直线运动,经过
,则F=15N,故A错误,B正确。若改变水平力F大小,使小球A由静止开始,向右做加速度大小为4.5m/s2的匀加速直线运动,经过![]() 时,A的速度为vA=at=3m/s,位移
时,A的速度为vA=at=3m/s,位移![]() ,则由几何关系可知,B上升1m,此时∠OAB=370,由速度的分解知识可知:vAcos370=vBcos530,解得vB=4m/s,即小球B的速度大小为4m/s,此段时间内拉力F的功为
,则由几何关系可知,B上升1m,此时∠OAB=370,由速度的分解知识可知:vAcos370=vBcos530,解得vB=4m/s,即小球B的速度大小为4m/s,此段时间内拉力F的功为![]() ,选项CD正确;故选BCD.
,选项CD正确;故选BCD.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目