题目内容
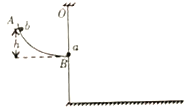
【题目】如图所示,AB为固定在竖直平面内的圆弧轨道,轨道末端B切线水平,质量ma=0.5kg的小球a用细线悬挂于O点,线长L=0.5m,细线能承受的最大拉力T=9N。质量mb=1kg的小球b从轨道上距底端B高度h=0.3m处由静止释放,与a球发生对心碰撞,碰后瞬间细线恰好被拉断。已知小球a、b落地的水平距离之比为2:1,g取10m/s2。
(1)细线被拉断瞬间小球a的速度;
(2)小球b在圆弧轨道上克服阻力所做的功W。
【答案】(1) ![]() (2)
(2) ![]()
【解析】(1)细线被拉断瞬间,对a球,由牛顿第二定律得![]() ①
①
由①式得va=2m/s
(2)设b球与a球碰前瞬间速度为vb,碰后瞬间b球速度为![]() ,
,
由动量守恒定律得:![]() ②
②
由题意得![]() ③
③
由②③式得:![]()
对b球,从A到B过程由动能定理得:![]()
由④式得:![]()

练习册系列答案
相关题目