题目内容
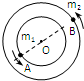
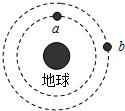
我国于2007年10月24日,在西昌卫星发射中心,将一颗探月卫星“嫦娥一号”成功发射升空,在经历14天的飞行后,“嫦娥一号”卫星接近月球,实施首次“制动变轨”,进入月球捕获椭圆轨道,又经历两次“制动变轨”,最终进入预定环月工作轨道(如图所示).
(1)卫星在靠近月球前先进行变轨,在预定点处启动卫星上的喷气推进器,为使卫星从椭圆轨道进入环月飞行圆轨道,如图所示,推进器是向前喷气还是向后喷气?
(2)若已知地球和月球的半径之比为
=3.6,地球和月球表面的重力加速度之比为
=6,求地球和月球的密度之比;
(3)若已知月球半径为R,月球表面处重力加速度为g,卫星在环月圆轨道上的运行周期为T,试求卫星在环月圆轨道上运行时离月球表面高度和卫星环月圆轨道处的重力加速度.

(1)卫星在靠近月球前先进行变轨,在预定点处启动卫星上的喷气推进器,为使卫星从椭圆轨道进入环月飞行圆轨道,如图所示,推进器是向前喷气还是向后喷气?
(2)若已知地球和月球的半径之比为
| R0 |
| R |
| g0 |
| g |
(3)若已知月球半径为R,月球表面处重力加速度为g,卫星在环月圆轨道上的运行周期为T,试求卫星在环月圆轨道上运行时离月球表面高度和卫星环月圆轨道处的重力加速度.

(1)“嫦娥一号”从椭圆轨道进入环月飞行圆轨道,做逐渐靠近圆心的运动,即做向心运动,应减速,故向前喷气.
(2)在星球表面,根据万有引力等于重力列出等式G
=mg,得M=
密度的定义式ρ=
所以ρ=
=
已知地球和月球的半径之比为
=3.6,表面的重力加速度之比为
=6,
所以地球和月球的密度之比
=
=
=
(3)“嫦娥一号”星绕月球做匀速圆周运动,根据万有引力提供向心力列出等式,G
=m
(R+h),得h=
-R
在月球表面,根据万有引力等于重力列出等式:G
=m′g,得GM=R2g,
所以:h=
-R
卫星环月圆轨道处,根据万有引力定律和牛顿第二定律G
=mgh,
得gh=
=
=
答:(1)推进器是向前喷气.
(2)地球和月球的密度之比为
.
(3)卫星在环月圆轨道上运行时离月球表面高度为
-R,卫星环月圆轨道处的重力加速度为
.
(2)在星球表面,根据万有引力等于重力列出等式G
| Mm |
| R2 |
| R2g |
| G |
密度的定义式ρ=
| M |
| V |
所以ρ=
| ||
|
| 3g |
| 4GπR |
已知地球和月球的半径之比为
| R0 |
| R |
| g0 |
| g |
所以地球和月球的密度之比
| ρ0 |
| ρ |
| g0R |
| gR0 |
| 6 |
| 3.6 |
| 5 |
| 3 |
(3)“嫦娥一号”星绕月球做匀速圆周运动,根据万有引力提供向心力列出等式,G
| Mm |
| (R+h)2 |
| 4π2 |
| T2 |
| 3 |
| ||
在月球表面,根据万有引力等于重力列出等式:G
| Mm′ |
| R2 |
所以:h=
| 3 |
| ||
卫星环月圆轨道处,根据万有引力定律和牛顿第二定律G
| Mm |
| (R+h)2 |
得gh=
| GM |
| (R+h)2 |
| R2g | |||||
(
|
| 3 |
| ||
答:(1)推进器是向前喷气.
(2)地球和月球的密度之比为
| 5 |
| 3 |
(3)卫星在环月圆轨道上运行时离月球表面高度为
| 3 |
| ||
| 3 |
| ||

练习册系列答案
相关题目