Question

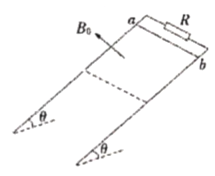
【题目】如图,间距为L=0.5m足够长的平行金属导致放置在与水平面间夹角为θ=37°的绝缘斜面上,导轨的上端连接有一个R=4Ω的电阻。有一个匀强磁场垂直于导轨平面向上,磁感应强度为B0=1T,将一根质量为m=0.05kg长度也为L的金属棒ab放置在导轨上并与其垂直,且与导轨接触良好,金属棒的电阻r=1Ω,导轨的电阻不计。金属棒与导轨间的动摩擦因数μ=0.5,静止释放金属棒,金属棒能沿导轨向下滑动。当流过金属棒截面的电量为0.3C时,金属棒恰达到稳定速度,(g-10m/s2，sin37°=0.6,cos37°=0.8)。则:

(1)金属棒达到的稳定速度是多少?

(2)从静止释放金属棒到其达到稳定速度过程中,电阻R上产生的焦耳热为多少?

(3)若将金属棒达到稳定速度时计作时间t=0,从此时刻起,让磁感应强B逐渐减小,使金属棒中不产生感应电流,则t=1s时磁感应强度为多大?

Answer 1

【答案】（1）2m/s（2）0.16J（3）0.5T

【解析】

（1）对金属棒进行受力分析，达到稳定速度时，即为做匀速运动，根据平衡条件列出等式求解．

（2）根据平均电动势和流过导体截面的电量值求解达到稳定速度之前导体棒下降的距离s；根据能量守恒得，重力势能减小转化为动能、摩擦产生的内能和回路中产生的焦耳热．再根据串联电路能量（功率）分配关系，就可求得电阻R上产生的热量．

（3）要使金属棒中不产生感应电流，则穿过线框的磁通量不变．同时棒受到重力、支持力与滑动摩擦力做匀加速直线运动．从而可求出磁感应强度B应怎样随时间t变化的，然后求出磁感应强度．

（1）在达到稳定速度前，金属棒的加速度逐渐减小，速度逐渐增大，达到稳定速度v时有：
感应电动势：E=B0Lv，由欧姆定律得：E=I（R+r），
安培力：FA=B0IL，

由平衡条件得：mgsinθ=FA+μmgcosθ，

代入数据解得：v=2m/s；
（2）根据

，

解得，解得s=3m

即金属棒达到稳定之前，导体棒下滑的距离为3m；根据能量守恒得，重力势能减小转化为动能、摩擦产生的内能和回路中产生的焦耳热．
由能量守恒定律得：mgssinθ=mv2+μmgscosθ+Q，
电阻R上产生的热量：QR=Q，代入数据解得：QR=0.16J；
（3）当回路中的总磁通量不变时，金属棒中不产生感应电流．
此时金属棒将沿导轨做匀加速运动，故：mgsinθ-μmgcosθ=ma
设t时刻磁感应强度为B，则：B0Ls=BL（s+x），
位移：x=vt+at2，解得，t=1s时磁感应强度：B=0.5T；