题目内容

如图所示，一光滑绝缘圆管轨道位于竖直平面内，半径为0.2m。以圆管圆心O为原点，在环面内建立平面直角坐标系xOy，在第四象限加一竖直向下的匀强电场，其他象限加垂直于环面向外的匀强磁场。一带电量为+1.0C、质量为0.1kg的小球（直径略小于圆管直径），从x坐标轴上的b点由静止释放，小球刚好能顺时针沿圆管轨道做圆周运动。（重力加速度g取10m/s2）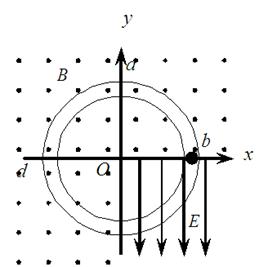

（1）求匀强电场的电场强度E；
（2）若第二次到达最高点a时，小球对轨道恰好无压力，求磁感应强度B ；
（3）求小球第三次到达最高点a时对圆管的压力。

(1)1N/C   (2)0.5T    (3) N

解析试题分析：（1）小球第一次刚好过最高点，此时速度v1=0
           2分
∴=1N/C            2分
（2）小球第二次过最高点是速度为，由动能定理可知
             2分
又              2分
以上两式可解得  =0.5T          1分
（3）小球第三次过最高点时速度为，小球受圆管向下的压力为FN
         2分
          2分
解得  N           1分
根据牛顿第三定律可知 小球第三次到达最高点a时对圆管的压力为N 方向竖直向上    1分
考点：本题考查动能定理和牛顿第二定律在带电粒子在匀强电场和匀强磁场中的运动的应用．

练习册系列答案
相关题目

（19分）如图，在区域I（0≤x≤d）和区域II（d≤x≤2d）内分别存在匀强磁场，磁感应强度大小分别为B和2B，方向相反，且都垂直于Oxy平面。一质量为m、带电荷量q（q＞0）的粒子a于某时刻从y轴上的P点射入区域I，其速度方向沿x轴正向。已知a在离开区域I时，速度方向与x轴正方向的夹角为30°；此时，另一质量和电荷量均与a相同的粒子b也从p点沿x轴正向射入区域I，其速度大小是a的1/3。不计重力和两粒子之间的相互作用力。求

（1）粒子a射入区域I时速度的大小；
（2）当a离开区域II时，a、b两粒子的y坐标之差。

(18分) 如图所示，区域Ⅰ中有竖直向上的匀强电场，电场强度为E； 区域Ⅱ内有垂直纸面向外的水平匀强磁场，磁感应强度为B；区域Ⅲ中有垂直纸面向里的水平匀强磁场，磁感应强度为2B。一质量为m、带电量为q的带负电粒子（不计重力）从左边界O点正上方的M点以速度v0水平射入电场，经水平分界线OP上的A点与OP成60°角射入Ⅱ区域的磁场，并垂直竖直边界CD进入Ⅲ区域的匀强磁场中。

求：（1）粒子在Ⅱ区域匀强磁场中运动的轨道半径；
（2）O、M间的距离；
（3）粒子从第一次进入区域Ⅲ到离开区域Ⅲ所经历的时间t3。

（22分）如图所示，在xoy坐标平面的第一象限内有一沿y轴负方向的匀强电场，在第四象限内有一垂直于平面向里的匀强磁场，现有一质量为m、电量为+q的粒子（重力不计）从坐标原点O射入磁场，其入射方向与y的方向成45°角。当粒子运动到电场中坐标为（3L，L）的P点处时速度大小为v0,方向与x轴正方向相同。求：

（1）粒子从O点射入磁场时的速度v；
（2）匀强电场的场强E0和匀强磁场的磁感应强度B0；
（3）粒子从O点运动到P点所用的时间.

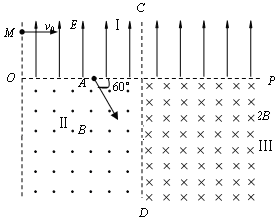
如图所示为带电平行板电容器．电容为c．板长为L，两板间距离d，在PQ板的下方有垂直纸面向里的匀强磁场．一个电荷量为、质量为m的带电粒子以速度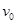从上板边缘沿平行于板的方向射入两板间．结果粒子恰好从下板右边缘飞进磁场，然后又恰好从下板的左边缘飞进电场．不计粒子重力．试求：

（1）板间匀强电场向什么方向?带电粒子带何种电荷?
（2）求出电容器的带电量Q
（3）匀强磁场的磁感应强度B的大小；
（4）粒子再次从电场中飞出时的速度大小和方向．

（18分）如图所示，在平面内的第一象限内存在沿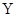轴正方向的匀强电场，在第四象限存在有界的磁场，磁感应强度，有一质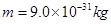量为，电量为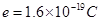的电子以的速度从轴的点（0，cm）沿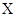轴正方向射入第一象限，偏转后从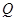轴的点射入第四象限，方向与轴成角，在磁场中偏转后又回到点，方向与轴也成角;不计电子重力.求：

（1）OQ之间的距离及电子通过Q点的速度大小.
（2）若在第四象限内的磁场的边界为直线边界，即在虚线的下方有磁场，如图中所示,求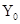的坐标.
（3）若在第四象限内的磁场为圆形边界的磁场，圆形边界的磁场的圆心坐标的范围.

（17分）如图甲所示,两平行金属板接有如图乙所示随时间t变化的电压U,两板间电场可看作均匀的,且两板外无电场,板长L="0.2" m,板间距离d="0.2" m．在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板中线OO′垂直,磁感应强度B=5×10 3T,方向垂直纸面向里．现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子速度v0=105 m/s,比荷q/m=108 C/kg,重力忽略不计,在每个粒子通过电场区域的极短时间内,电场可视作是恒定不变的．

（1）试求带电粒子射出电场时的最大速度;
（2）从电场射出的带电粒子,进入磁场运动一段时间后又射出磁场,求粒子在磁场中运动的最长时间和最短时间．

（12分）如图所示，水平绝缘轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接，半圆形轨道的半径R=0.40m。轨道所在空间存在水平向右的匀强电场，电场强度E=1.0×104N/C。现有一电荷量q=+1.0×10 4C，质量m=0.10kg的带电体（可视为质点），在水平轨道上的P点由静止释放，带电体恰好能够通过最高点C,已知带电体与水平轨道间的动摩擦因数μ=0.50，重力加速度g=10m/s2。求：

（1）带电体运动到圆形轨道的最低点B时，圆形轨道对带电体支持力的大小；
（2）带电体在水平轨道上的释放点P到B点的距离；
（3）带电体第一次经过C点后，落在水平轨道上的位置到B点的距离。

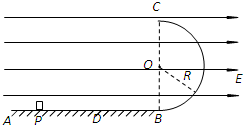
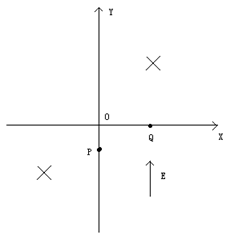
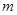（19分）如图所示，在坐标系xoy的第一、第三象限内存在相同的匀强磁场，磁场方向垂直于xoy面向里；第四象限内有沿y轴正方向的匀强电场，电场强度大小为E. 一质量为、带电量为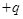的粒子自y轴的P点沿x轴正方向射入第四象限，经x轴上的Q点进入第一象限，随即撤去电场，以后仅保留磁场。已知OP=d,OQ=2d,不计粒子重力。

（1）求粒子过Q点时速度的大小和方向。
（2）若磁感应强度的大小为一定值B0，粒子将以垂直y轴的方向进入第二象限，求B0；
（3）若磁感应强度的大小为另一确定值，经过一段时间后粒子将再次经过Q点，且速度与第一次过Q点时相同，求该粒子相邻两次经过Q点所用的时间。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网