题目内容
(18分)图所示为回旋加速器的示意图。它由两个铝制D型金属扁盒组成,两个D形盒正中间开有一条狭缝,两个D型盒处在匀强磁场中并接在高频交变电源上。在D1盒中心A处有离子源,它产生并发出的a粒子,经狭缝电压加速后,进入D2盒中。在磁场力的作用下运动半个圆周后,再次经狭缝电压加速。为保证粒子每次经过狭缝都被加速,设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致。如此周而复始,速度越来越 大,运动半径也越来越大,最后到达D型盒的边缘,以最大速度被导出。已知a粒子电荷量为q,质量为m,加速时电极间电压大小恒为U,磁场的磁感应强度为B,D型盒的半径为R,设 狭 缝 很 窄,粒子通过狭缝的时间可以忽略不计,设α粒子从离子源发出时的初速度为零。(不计α粒子重力)求: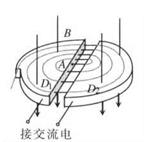
(1) α粒子第一次被加速后进入D2盒中时的速度大小;
(2) α粒子被加速后获得的最大动能Ek和交变电压的频率f;
(3)α粒子在第n次由D1盒进入D2盒与紧接着第n+1次由D1盒进入D2盒位置之间的距离Δx。
(1)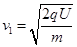 (2)
(2)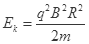 ,
,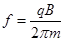 (3)
(3)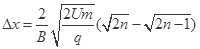
解析试题分析:α粒子在狭缝中做加速运动,在D形盒内做匀速圆周运动。
(1)设α粒子第一次被加速后进入D2盒中时的速度大小为v1,根据动能定理有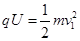 2分
2分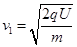 2分
2分
(2)α粒子在D形盒内做圆周运动,轨道半径达到最大时被引出,具有最大动能。设此时的速度为vm,有  2分
2分
解得: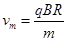 2分
2分
设α粒子的最大动能为Ek,则
Ek= 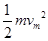 2分
2分
解得:Ek=  2分
2分
设交变电压的周期为T、频率为f,为保证粒子每次经过狭缝都被加速,带电粒子在磁场中运动一周的时间应等于交变电压的周期(在狭缝的时间极短忽略不计),则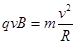 ,
,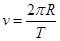
解得:T=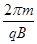 1分
1分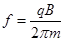 1分
1分
(3)离子经电场第1次加速后,以速度 进入D2盒,设轨道半径为r1
进入D2盒,设轨道半径为r1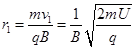
离子经第2次电场加速后,以速度v2进入D1盒,设轨道半径为r2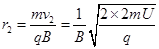 1分
1分
离子第n次由D1盒进入D2盒,离子已经过(2n-1)次电场加速,以速度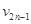 进入D2盒,由动能定理:
进入D2盒,由动能定理: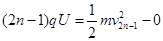
解得轨道半径: 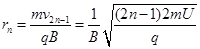 1分
1分
离子经第n+1次由D1盒进入D2盒,离子已经过2n次电场加速,以速度v2n进入D1盒,由动能定理: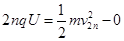
轨道半径: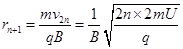 1分
1分
则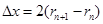 1分(如图所示)
1分(如图所示)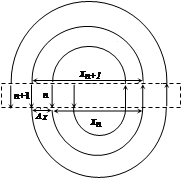
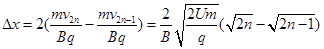 1分
1分
考点:回旋加速器 带电粒子在磁场中匀速圆周运动 动能定理 周期和频率

 阅读快车系列答案
阅读快车系列答案在光滑水平面上推物块和在粗糙水平面上推物块相比较,如果所用的水平推力相同,物块在推力作用下通过的位移相同,则推力对物块所做的功
| A.一样大 | B.在光滑水平面上推力所做的功较多 |
| C.在粗糙水平面上推力所做的功较多 | D.要由物块通过这段位移的时间决定 |
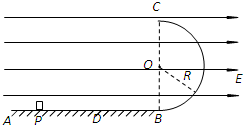
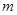 、带电量为
、带电量为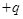 的粒子自y轴的P点沿x轴正方向射入第四象限,经x轴上的Q点进入第一象限,随即撤去电场,以后仅保留磁场。已知OP=d,OQ=2d,不计粒子重力。
的粒子自y轴的P点沿x轴正方向射入第四象限,经x轴上的Q点进入第一象限,随即撤去电场,以后仅保留磁场。已知OP=d,OQ=2d,不计粒子重力。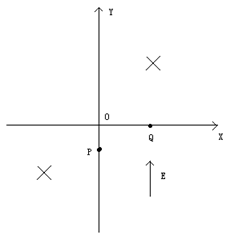
 平面第一象限整个区域分布匀强电场,电场方向平行
平面第一象限整个区域分布匀强电场,电场方向平行 轴向下,在第四象限内存在有界匀强磁场,左边界为
轴向下,在第四象限内存在有界匀强磁场,左边界为 的直线,磁场方向垂直纸面向外。质量为
的直线,磁场方向垂直纸面向外。质量为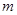 、带电量为
、带电量为 的粒子从
的粒子从 点以初速度
点以初速度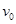 垂直
垂直 轴上
轴上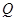 点以与
点以与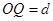 ,不计粒子重力。求:
,不计粒子重力。求:
 的取值范围;
的取值范围; 的匀强磁场中。已知匀强电场的宽度为d=
的匀强磁场中。已知匀强电场的宽度为d= R,匀强磁场由一个长为2R、宽为
R,匀强磁场由一个长为2R、宽为

 消耗的功率为
消耗的功率为 ,求该速度的大小;
,求该速度的大小;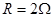 ,金属棒中的电流方向
,金属棒中的电流方向 到
到 ,求磁感应强度的大小与方向。(
,求磁感应强度的大小与方向。(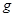 取
取 ,
, ,
,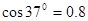 )
)
 的电阻。在虚线OO′(OO′垂直于轨道)右侧有方向竖直向下的匀强磁场,磁感应强度B=0.50T。一根质量m=0.10kg的直金属杆
的电阻。在虚线OO′(OO′垂直于轨道)右侧有方向竖直向下的匀强磁场,磁感应强度B=0.50T。一根质量m=0.10kg的直金属杆 垂直于轨道放在两根轨道上。某时刻杆
垂直于轨道放在两根轨道上。某时刻杆 =2.0m/s且平行于轨道的初速度进入磁场,同时在杆上施加一个水平拉力,使其以
=2.0m/s且平行于轨道的初速度进入磁场,同时在杆上施加一个水平拉力,使其以 =2.0m/s2的加速度做匀减速直线运动。杆
=2.0m/s2的加速度做匀减速直线运动。杆
 时,水平拉力的大小;
时,水平拉力的大小;