��Ŀ����
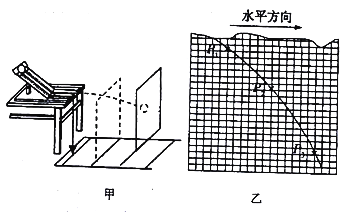
����Ŀ����ͼ��ʾ������б��Ϊ30���Ĺ⻬б���Ͼ�ֹ����![]() ����С�����ǵ������ֱ�ΪM��m�����ǵİ뾶�ֱ�ΪR��r������֮���ó�Ϊ
����С�����ǵ������ֱ�ΪM��m�����ǵİ뾶�ֱ�ΪR��r������֮���ó�Ϊ![]() ������������ͼ��δ����������ʼʱ
������������ͼ��δ����������ʼʱ![]() ������һ��������б���ϵ�A������б���ϵ�B���̶�һ������С�ĵ��壬С�װ뾶ΪR0(r<R0<R)��A��B�����Ϊ
������һ��������б���ϵ�A������б���ϵ�B���̶�һ������С�ĵ��壬С�װ뾶ΪR0(r<R0<R)��A��B�����Ϊ![]() ���ֽ����С�����������
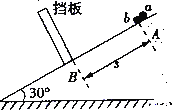
���ֽ����С�����������![]() ��С��һ��Ӿ�ֹ��ʼ��б���»���b��ȡ�谭��ͨ��С�ף���a���뵲�巢����е��ʧ����ײ��a����ײ����б�������˶���b������б�������˶�������������ʱ�伫�̣�б���㹻������С��ʼ����б�����˶����������ٶ�gȡ10m/s2��
��С��һ��Ӿ�ֹ��ʼ��б���»���b��ȡ�谭��ͨ��С�ף���a���뵲�巢����е��ʧ����ײ��a����ײ����б�������˶���b������б�������˶�������������ʱ�伫�̣�б���㹻������С��ʼ����б�����˶����������ٶ�gȡ10m/s2��
(1)��С��![]() ��A���ɾ�ֹ��ʼһ���������»��ļ��ٶȴ�С�����ǵ��ﵲ����ٶ�
��A���ɾ�ֹ��ʼһ���������»��ļ��ٶȴ�С�����ǵ��ﵲ����ٶ�![]() �Ĵ�С��
�Ĵ�С��
(2)��![]() ��������
��������![]() �����������˲�䣬
�����������˲�䣬 ![]() ����ͬ�ٶ�v�Ĵ�С�ͷ���
����ͬ�ٶ�v�Ĵ�С�ͷ���
(3)��![]() ������������ͬ�ٶ�v�ķ�����kֵ��ϵ��
������������ͬ�ٶ�v�ķ�����kֵ��ϵ��
���𰸡�(1) ![]() (2)
(2) ![]() ������������� (3)��
��������б������ (3)��![]() ʱ,�ٶ�Ϊ�㣻��
ʱ,�ٶ�Ϊ�㣻��![]() ʱ��v��б�����ϣ���
ʱ��v��б�����ϣ���![]() ʱ,v��б��������
ʱ,v��б��������
����������1����![]() ����һ���˶��ļ��ٶȴ�СΪa����ţ�ٵڶ����ɵõ���
����һ���˶��ļ��ٶȴ�СΪa����ţ�ٵڶ����ɵõ��� ![]()
��ã� ![]()
���ȱ���ֱ���˶����ɿ�֪�� ![]()
��ã� ![]() ��
��
��2��a���뵲�巢�����е����ʧ����ײ���ٶ�Ϊ![]() ������������ǰ˲��С��
������������ǰ˲��С��![]() ���ٶȴ�СΪ
���ٶȴ�СΪ![]() ��
��![]() ��������С������������ʱ��Ϊt����һ����������ļ��ٶ���ͬ��b�����a��Ϊ�����˶������У�
��������С������������ʱ��Ϊt����һ����������ļ��ٶ���ͬ��b�����a��Ϊ�����˶������У� ![]()
��a�� ![]() ����b��
����b�� ![]()
��ã� ![]() ��������б�����£�
��������б�����£�
![]() ��������б�����ϣ�
��������б�����ϣ�
������������ʱ�伫�̣�����������б�淽��ķ�����ȡ��б������Ϊ�������ɶ����غ㶨�ɵõ���
![]()
��![]() ʱ����ã�
ʱ����ã� ![]() ��������б�����£�
��������б�����£�
��3����![]() ���ɣ�2���ʿ�֪��
���ɣ�2���ʿ�֪�� ![]()
��![]() ʱ��
ʱ�� ![]()
���ۣ���![]() ʱ��������˲�䣬
ʱ��������˲�䣬 ![]() ����˲ʱ�ٶ�Ϊ�㣻
����˲ʱ�ٶ�Ϊ�㣻
��![]() ʱ��
ʱ�� ![]() ����������
���������� ![]() ������б�������˶���
������б�������˶���
��![]() ʱ��
ʱ�� ![]() ����������
���������� ![]() ������б�������˶���
������б�������˶���

 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�