题目内容
1. 如图所示,跨过同一高度处的定滑轮的细线连接着质量相同的物体A和B,A套在光滑水平杆上,定滑轮离水平杆的高度h=0.2m,开始时让连着A的细线与水平杆的夹角θ=37°,由静止释放B,在运动过程中,A所获得的最大速度为多大?(设B不会碰到水平杆,sin37°=0.6,sin53°=0.8,取g=10m/s2)
如图所示,跨过同一高度处的定滑轮的细线连接着质量相同的物体A和B,A套在光滑水平杆上,定滑轮离水平杆的高度h=0.2m,开始时让连着A的细线与水平杆的夹角θ=37°,由静止释放B,在运动过程中,A所获得的最大速度为多大?(设B不会碰到水平杆,sin37°=0.6,sin53°=0.8,取g=10m/s2)
分析 将A的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向上的分速度等于B的速度大小,根据该关系得出A、B的速率之比.当θ=90°时,A的速率最大,此时B的速率为零,根据动能定理求出A获得的最大速度.
解答 解:将A的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向上的分速度等于B的速度大小,有:vAcosθ=vB,当θ=90°时,A的速率最大,此时B的速率为零.根据动能定理:${m}_{B}g(\frac{h}{sin37°}-h)=\frac{1}{2}m{v}_{A}^{2}$,
解得:vA=$2\sqrt{\frac{2}{3}}$m/s.
答:A所获得的最大速度为$2\sqrt{\frac{2}{3}}$m/s.
点评 解决本题的关键知道A沿绳子方向上的分速度等于B的速度大小,以及知道A、B组成的系统机械能守恒.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
11.物体从斜面底端由某初速度开始恰能匀变速上滑顶端,经时间t到达斜面中点,则物体从斜面底端到顶端共用时间为( )
| A. | ($\sqrt{2}$-1)t | B. | ($\sqrt{2}$+2)t | C. | 2t | D. | ($\sqrt{2}$+1)t |
12.作用在同一物体上的99个力,恰使物体处于匀速直线运动状态,若将其中两个6N和8N的力撤去,其余的97个力的合力大小可能是( )
| A. | 1N | B. | 3N | C. | 13 N | D. | 15N |
6. 如图所示,实线为一匀强电场的电场线,一个带负电的粒子射入电场后,留下一条从a到b虚线所示径迹,重力不计,下列判断正确的是( )
如图所示,实线为一匀强电场的电场线,一个带负电的粒子射入电场后,留下一条从a到b虚线所示径迹,重力不计,下列判断正确的是( )
 如图所示,实线为一匀强电场的电场线,一个带负电的粒子射入电场后,留下一条从a到b虚线所示径迹,重力不计,下列判断正确的是( )
如图所示,实线为一匀强电场的电场线,一个带负电的粒子射入电场后,留下一条从a到b虚线所示径迹,重力不计,下列判断正确的是( )| A. | b点电势高于a点电势 | |
| B. | 场强方向向左 | |
| C. | 粒子在a点的动能大于在b点的动能 | |
| D. | 粒子在a点的电势能小于在b点的电势能 |
13.在做“研究平抛运动”的实验时,让小球多次沿同一轨道运动,通过描点法画出小球做平抛运动的轨迹.为了能较准确地描绘运动轨迹,下列说法正确的是( )
| A. | 通过调节使斜槽的末端保持水平 | |
| B. | 每次必须由静止释放小球 | |
| C. | 每次释放小球的位置必须不同 | |
| D. | 将球经过不同高度的位置记录在纸上后,取下纸,用直尺将点连成折线 |
10.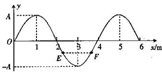 一列波沿x轴正向传播,t=0时刻的波形如图所示,其中E、F两点相对平衡位置的位移相同,从该时刻起E质点回到平衡位置的最短时间为0.05s.F质点回到平衡位置的最短时间为0.15s,质点的振幅为A=10cm,则下列说法正确的是 ( )
一列波沿x轴正向传播,t=0时刻的波形如图所示,其中E、F两点相对平衡位置的位移相同,从该时刻起E质点回到平衡位置的最短时间为0.05s.F质点回到平衡位置的最短时间为0.15s,质点的振幅为A=10cm,则下列说法正确的是 ( )
 一列波沿x轴正向传播,t=0时刻的波形如图所示,其中E、F两点相对平衡位置的位移相同,从该时刻起E质点回到平衡位置的最短时间为0.05s.F质点回到平衡位置的最短时间为0.15s,质点的振幅为A=10cm,则下列说法正确的是 ( )
一列波沿x轴正向传播,t=0时刻的波形如图所示,其中E、F两点相对平衡位置的位移相同,从该时刻起E质点回到平衡位置的最短时间为0.05s.F质点回到平衡位置的最短时间为0.15s,质点的振幅为A=10cm,则下列说法正确的是 ( )| A. | 这列渡的周期为0.4s | |
| B. | E点在t=0时偏离平衡位置的距离为$\frac{A}{2}$ | |
| C. | 该渡的传播速度为10m/s | |
| D. | E质点在4s内运动的路程为40m | |
| E. | 该波很容易绕过0.4m的障碍物 |
11.关于人造地球卫星的说法中正确的是( )
| A. | 同步通讯卫星的高度和速率是可变的,高度增加速率增大,仍然同步 | |
| B. | 所有的同步卫星的高度和速率都是一定的,且它们都在赤道上空的同一轨道上运行 | |
| C. | 欲使某颗卫星的周期比预计的周期增大2倍,可使原来预算的轨道半径r变为$\sqrt{4}r$ | |
| D. | 欲使卫星的周期比预计的周期增大到原来的2倍,可使原来的轨道半径不变,使速率增大到原来预计的2倍 |