Question

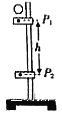
【题目】如图所示，一个足够长的斜面，AC部分的长度为4L，C点以下光滑，C点以上粗糙，B是AC的中点。一根原长为2L的轻弹簧下端固定在A点，上端放置一个长为L、质量为m的均匀木板PQ，木板静止时，弹簧长度变为L。已知斜面的倾角为，木板与斜面粗糙部分的动摩擦因数，木板受到的最大静摩擦力等于滑动摩擦力，重力加速度为g。现将木板沿斜面缓慢下压，当弹簧长度变为L时，释放木板，发现木板的Q端刚好能到达C点；将木板截短后，再次将木板沿斜面缓慢下压，当弹簧长度变为L时，释放木板，求：

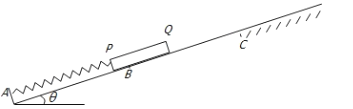
⑴弹簧的劲度系数；

⑵若木板被截掉一半，木板上端到达C点时的速度大小；

⑶至少要将木板截掉多少，木板被释放后能静止在斜面上？

Answer 1

【答案】(1) ；(2) ；(3)

【解析】

当木板静止时，对木板受力分析，运用平衡条件和胡克定律求弹簧的劲度系数；木板从被释放至Q端到C点，利用动能定理列式．木板被截掉一半后再被弹簧弹开，再运用动能定理列式，联立可得木板上端到达C点时的速度；木板剩下的越短，被弹簧弹开后越能静止在斜面上．木板被弹开后恰好可以静止在斜面上时，重力沿斜面向下的分力等于最大静摩擦力．由此列式可得到截掉后剩余木板有一半在C点以上就可静止在斜面上．再由动能定理求解。

⑴当木板静止时，对木板受力分析，由力的平衡有

解得弹簧的劲度系数

⑵木板从被释放至Q端到C点，设弹簧弹力做功为W，由动能定理有

木板被截掉一半后再被弹簧弹开，设木板上端到达C点时的速度为v，由动能定理有

解以上两式得：

⑶木板剩下的越短，被弹簧弹开后越能静止在斜面上。

设木板长为x时被弹开后恰好可以静止在斜面上，此木板必然一部分在C点上方，一部分在C点下方。假设在C点上方的木板长度为a，则有

解得

这表明，截掉后剩余木板有一半在C点以上就可静止在斜面上。剩余木板被弹开后直到静止的过程中，由动能定理有

解得：

即木板被截下的长度至少为