题目内容
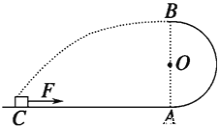
【题目】如图所示，竖直平面内有一个半径为R的圆周，另外空间有一平行于圆周平面的匀强电场，A、D两点为圆周上和圆心同一高度的点，C点为圆周上的最高点。在与OA夹角为
的圆弧B点上有一粒子源，以相同大小的初速度v0在竖直面（平行于圆周面）内沿各个方向发射质量为m，带电的同种微粒，在对比通过圆周上各点的微粒中，发现从圆周D点上离开的微粒机械能最大，从圆周E点（OE与竖直方向夹角
）上离开的微粒动能最大，已知重力加速度为
，取最低点F所在水平面为重力零势能面。则有（ ）
A.电场一定沿OD方向，且电场力等于
mg
B.通过E点的微粒动能大小为(
＋1)mgR＋
mv
C.动能最小的点可能在BC圆弧之间
D.A点的动能一定小于B点
【答案】BC
【解析】
AB．在D点微粒机械能最大，说明B到D电场力做功最大，由数学关系知过D点做圆的切线为电场的等势线，即电场力沿OD方向，带电粒子电性未知，场强方向不能确定。
在E点微粒动能最大，说明B到E合力做功最多，即重力电场力的合力方向沿OE，有
解得
动能定理有
故选项A错误、B正确；
C．OE反向延长线与圆的交点，为等效重力的最高点，合力做的负功最大，动能最小，选项C正确；
D．B点到A点等效重力（合力）做正功，动能增加，选项D错误。
故选BC。
练习册系列答案
相关题目
