题目内容
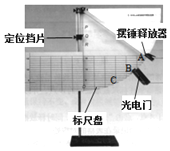
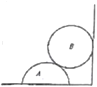
【题目】如图所示,竖直面光滑的墙角有一个质量为m,半径为r的半球体均匀物块A,现在A上放一质量为2m、半径同为r的光滑球体B,调整A 的位置使得A、B保持静止状态,已知A与地面间的动摩擦因数为0.5。
则A球球心距墙角的最远距离是( )
A. 2r
B. ![]()
C. ![]()
D. ![]()
【答案】C
【解析】
当地面对A的摩擦力达到最大静摩擦力时,A球球心距墙角的距离最远,AB处于静止状态,受力平衡,分别对A和B受力分析,根据平衡条件结合几何关系求解即可.
根据题意可知,B的质量为2m,AB处于静止状态,受力平衡,则地面对A的支持力为:N=3mg,当地面对A的摩擦力达到最大静摩擦力时,A球球心距墙角的距离最远,对A、B受力分析,如图所示;

根据平衡条件得:![]() ,Fcosθ=μ3mg,解得:tanθ=
,Fcosθ=μ3mg,解得:tanθ=![]() ;则A球球心距墙角的最远距离为:x=2rcosθ+r=
;则A球球心距墙角的最远距离为:x=2rcosθ+r=![]() r,故C正确,ABD错误。故选C。
r,故C正确,ABD错误。故选C。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目