题目内容
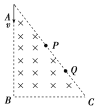
【题目】如图所示，斜面ABC下端与光滑的圆弧轨道CDE相切于C，整个装置竖直固定，D是最低点，圆心角∠DOC=37°，E、B与圆心O等高，圆弧轨道半径R=0.30m，斜面长L=1.90m，AB部分光滑，BC部分粗糙。现有一个质量m=0.10kg的小物块P从斜面上端A点无初速下滑，物块P与斜面BC部分之间的动摩擦因数
=0.75。取sin37o=0.6，cos37o=0.8，重力加速度g=10m/s2，忽略空气阻力。求：
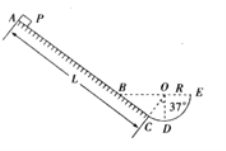
（1）物块第一次通过B点时的速度大小；
（2）物块第一次通过D点时受到轨道的支持力大小；
（3）物块最终所处的位置。
【答案】（1）
（2）
（3）x=0.35m
【解析】
(1)根据几何关系得，斜面BC部分的长度为：
设物块第一次通过B点时的速度为vB，根据动能定理有：
，代入数据解得：
。
(2)设物块第一次通过D点时的速度为vD，根据动能定理有：
，在D点由牛顿第二定律得：
代入数据得：
(3)物块每通过一次BC部分减少的机械能为：
物块在B点动能为：
物块能经过BC部分的次数为：
设物块第四次从下端进入BC部分后最终在距离C点x处静止，全程动能定理有：
，代入数据得：x=0.35m。
阅读快车系列答案
【题目】某同学在用电流表和电压表测电池的电动势和内阻的实验中，实验电路如图所示，为了防止因电池的内阻可能较小，在调节时造成电流过大，电路中用一个定值电阻R0起保护作用。除电池、开关和导线外，可供使用的器材还有：
（a）电流表（量程0.6A、3A）
（b）电压表（量程3V、15V）
（c）定值电阻（阻值1Ω、额定功率5W）
（d）定值电阻（阻值10Ω、额定功率10W）
（e）滑动变阻器（阻值范围0～10Ω、额定电流2A）
（f）滑动变阻器（阻值范围0～100Ω、额定电流1A）
请回答下列问题：
（1）要正确完成实验，电压表的量程应选择_______V，电流表的量程应选择_____A；R0应选择______Ω的定值电阻，R应选择阻值范围是________Ω的滑动变阻器。
（2）测得下列五组数据：根据数据在坐标图上画出U-I图像。
U/v | 1.60 | 1.40 | 1.20 | 1.00 | 0.80 |
I/A | 0.13 | 0.20 | 0.27 | 0.33 | 0.40 |
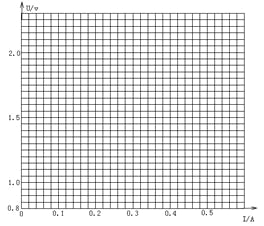
（3）据画出的图线求出电池电动势_____V，内阻_____Ω。（保留两位有效数字）
